1 时序差分学习
蒙特卡罗强化学习算法通过考虑采样轨迹,克服了模型未知给策略估计造成的困难。此类算法需在完成一个采样轨迹后再更新策略的值估计。而前而介绍的基于动态规划的策略迭代和值迭代算法在每执行一步策略后就进行值函数更新。两者相比,蒙特卡罗强化学习算法的效率低得多,这里的主要问题是:蒙特卡罗强化学习算法没有充分利用强化学习任务的 MDP 结构。
时序差分 (Temporal Difference ,简称 TD) 学习则结合了动态规划与蒙特卡罗方法的思想,能做到更高效的免模型学习。从算法的主体结构来看,它同蒙特卡罗类似,同样通过模拟交互序列的方式进行求解;但是从算法的核心思想来看,它同时用到了强化学习中的经典公式:Bellman公式进行自迭代更新。
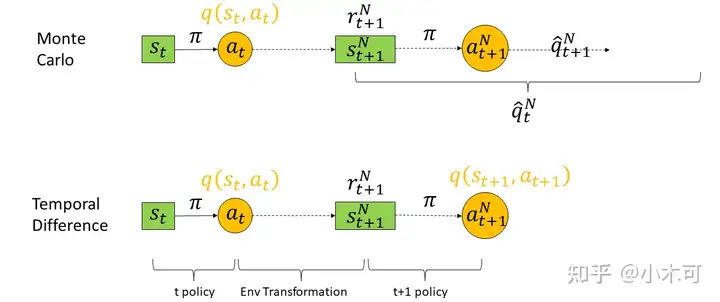
图1. Monte Carlo 和 Temporal Difference方法
蒙特卡罗强化学习算法的本质,是通过多次尝试后求平均来作为期望累积奖赏的近似,但它在求平均时是“批处理式”进行的,即在一个完整的采样轨迹完成后再对所有的状态-动作对进行更新。
实际上这个更新过程能增量式进行,由【原文1】公式(5)
$(1)qtN=qtN−1+1N∗(qtN−qtN−1)=qtN−1+1N∗(rt+1N+γqt+1N−qtN−1)$
其中: $qt+1N$表示对 $N$ 条轨迹, $t+1$ 时刻之后的奖赏之和。
根据 $qt+1N$取值不同, 时序差分学习Q−learning与 Sarsa算法。 两种算法都是基于 Qtable的算法。 Q−Learning属于离线学习(off-policy), Sarsa属于在线学习(on-policy)。
Sarsa
对Sarsa来说: 在状态 $st$ 下, 根据某策略(如 $ϵ−$ greedy策略)执行动作 $at$ 到达 $st+1$ 之后, 此时用来更新 $q(st,at)$ 的 $q$ 值的方法依然采用某策略(如 $ϵ−$ greedy策略),并且真正采取 $(st+1,a)$ 。
当进行单步迭代时, $qt+1N$并未改变,于是可用 $qt+1N−1$ 代替 $qt+1N$,同时用$α$ 替换$1N$,公式(1)可记为:
$(2)q(st,at)←q(st,at)+α∗[rt+1+γq(st+1,at+1)−q(st,at)]$
这就是TD法的基本形式,也被称为Sarsa算法。Sarsa这个名字来源于五个关键因子:S(State 当前状态 $st$ )、A(Action 当前行动 $at$ ) 、R(Reward 即时奖励 $rt+1$ )、S(State 下一时刻的状态 $st+1$ )和A(Action 下一时刻的行动 $at+1$ )。
Sarsa算法的具体实现流程如图2所示:

图2. Sarsa
Sarsa选取动作和更新Q表值得方法相同(均为 $ϵ−$ greedy策略),称为在线学习(on-policy)。
Q-Learning
对Q-Learning来说: 在状态 $st$ 下, 根据某策略(如 $ϵ−$ greedy策略)执行动作 $at$ 到达 $st+1$ 之后, 利用在状态 $st+1$ 下利用贪心策略采取所有动作中最大的那个 $q(st+1,a)$ ,来更新 $q(st,at)$ ,但是其并不真正采取 $(st+1,a)$。
Q-Learning的更新公式为:
$(3)q(st,at)←q(st,at)+α∗[rt+1+γmaxaq(st+1,a)−q(st,at)]$
具体实现流程如图3所示:

图3. Q-Learning
Q-Learning选取动作和更新Q表值得方法不同(选取动作为 $ϵ−$ greedy策略,更新Q表为贪心策略),称为离线学习(off-policy)。
2 代码实例
Sarsa实现代码为:
class SARSA:
def __init__(self, epsilon=0.0):
self.epsilon = epsilon
def sarsa_eval(self, agent, env):
state = env.reset()
while True:
# choose action
action = agent.epsilon_greedy_policy(state, self.epsilon)
next_state, reward, terminate, _ = env.step(action)
# on policy
next_action = agent.epsilon_greedy_policy(next_state, self.epsilon)
# update q table
agent.value_n[state][action] += 1
agent.value_q[state][action] += (reward + agent.gamma * agent.value_q[next_state][next_action] -
agent.value_q[state][action]) / \
agent.value_n[state][action]
if terminate:
break
state = next_state
def iteration(self, agent, env):
for i in range(10):
for j in range(2000):
self.sarsa_eval(agent, env)
agent.policy_improve()
return agent.pi
Q-Learning实现代码为
import numpy as np
class QLearning(object):
def __init__(self, epsilon=0.0):
self.epsilon = epsilon
def q_learn_eval(self, agent, env):
state = env.reset()
while True:
# choose action
action = agent.epsilon_greedy_policy(state, self.epsilon)
next_state, reward, terminate, _ = env.step(action)
# off policy
# update q table
agent.value_n[state][action] += 1
agent.value_q[state][action] += (reward + agent.gamma * np.max(agent.value_q[next_state, :]) -
agent.value_q[state][action]) / \
agent.value_n[state][action]
if terminate:
break
state = next_state
def iteration(self, agent, env):
for i in range(10):
for j in range(3000):
self.q_learn_eval(agent, env)
agent.policy_improve()
return agent.pi
使用Sarsa和Q-Learning求解蛇棋游戏过程为:
class SnakeRun(object):
@staticmethod
@time_wrapper
def sarsa_demo():
env = SnakeEnv()
agent = ModelFreeAgent(env)
mc = SARSA(0.5)
with timer('Timer sarsa Iter'):
mc.iteration(agent, env)
print('return_pi={}'.format(SnakeClient.run_episodes(env, agent.pi)))
print(agent.pi)
env.render_policy(agent.pi, render=False)
@staticmethod
@time_wrapper
def qlearning_demo():
env = SnakeEnv()
agent = ModelFreeAgent(env)
mc = QLearning(0.5)
with timer('Timer q learning Iter'):
mc.iteration(agent, env)
print('return_pi={}'.format(SnakeClient.run_episodes(env, agent.pi)))
print(agent.pi)
env.render_policy(agent.pi, render=True)
结果为:
*********** sarsa_demo
ladders info: {4: 17, 10: 32, 30: 51, 62: 80, 26: 83, 8: 39, 59: 66, 79: 87, 17: 4, 32: 10, 51: 30, 80: 62, 83: 26, 39: 8, 66: 59, 87: 79}
Timer sarsa Iter: 73.742 s
return_pi=(1000, 76)
[1 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 1 0 0 0 0 1 0 0 0 0 0
1 1 1 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1
1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0]
sarsa_demo: 76.311 s
*********** qlearning_demo
ladders info: {4: 17, 10: 32, 30: 51, 62: 80, 26: 83, 8: 39, 59: 66, 79: 87, 17: 4, 32: 10, 51: 30, 80: 62, 83: 26, 39: 8, 66: 59, 87: 79}
Timer q learning Iter: 111.159 s
return_pi=(1000, 76)
[1 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 1 0 0 0 0 0 1 1 1 1 0
0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1
1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0]
qlearning_demo: 113.538 s
Sarsa和Q-Learning的策略如图4和图5所示,
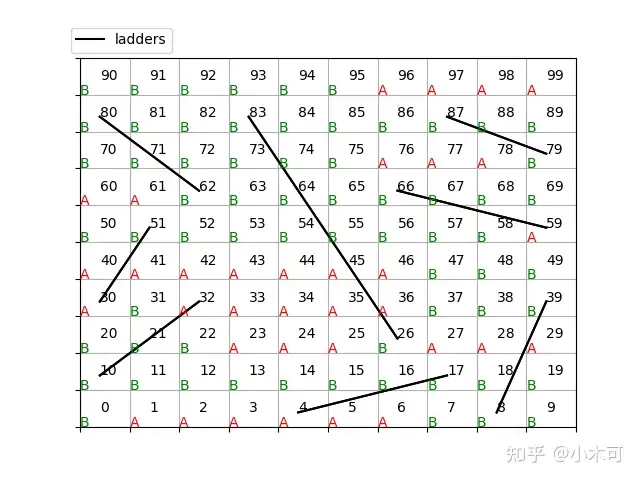
图4. 8个梯子的蛇棋Sarsa策略图
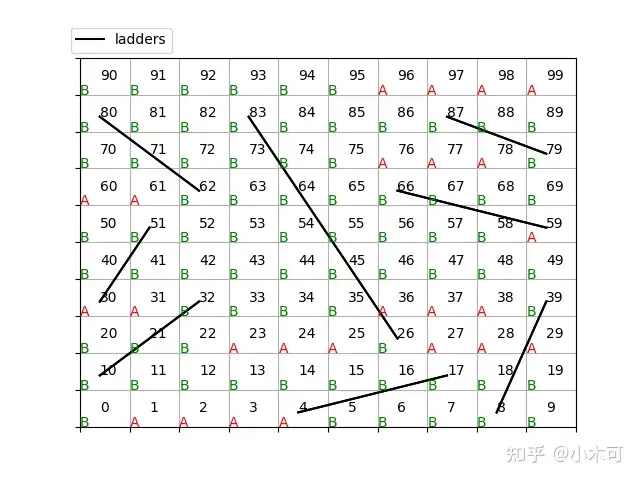
图5. 8个梯子的蛇棋SarsaQ-Learning图
几种Model-based和Model-free算法的运行结果统计如下:
策略迭代法价值迭代法泛化迭代法蒙特卡罗法Sarsa法Q-Learning法方法类型Model-basedModel-basedModel-basedModel-freeModel-freeModel-free特点单步更新单步更新单步更新回合更新单步更新单步更新训练总耗时(s)4.7504.5413.2646.69176.311113.538测试平均奖励767676757676
表1. 不同方法结果比较
可看出:
1) Sarsa和Q-Learning方法均为Model-free方法, 其训练总耗时明显高于Model-based方法(策略迭代法,价值迭代法,泛化迭代法),也明显高于基于回合更新的蒙特卡罗法。
2) 测试阶段,Model-free方法也能达到Model-based方法相同的性能(平均累计奖赏为76)。
3)Sarsa和Q-Learning方法的输出策略与Model-based方法输出的策略略有不同。这也说明,蛇棋的最优解并不唯一。
本文代码详见Github:TemporalDifference