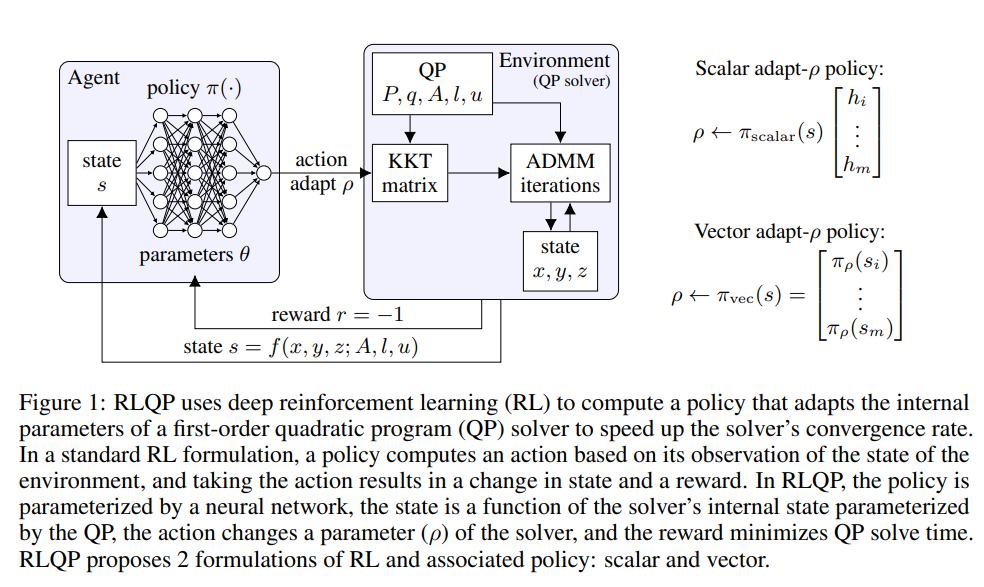
二次优化的一阶方法(如OSQP)被广泛用于大规模机器学习和嵌入式最优控制,其中许多相关问题必须快速解决。这些方法面临两个持续的挑战:手动超参数调整和高精度解的收敛时间。为了解决这些问题,我们探索强化学习(RL)如何学习策略来调整参数以加速收敛。在使用知名QP基准的实验中,我们发现我们的RL策略RLQP显著优于最先进的QP求解器3倍。RLQP令人惊讶地很好地概括了以前从未见过的问题,这些问题具有来自不同应用程序的不同维度和结构,包括QPLIB、Netlib LP和Maros-Mészáros问题。

有效地求解二次规划(QP)对于金融、机器人控制和运筹学的应用至关重要。尽管最先进的内点方法在问题维度上的伸缩性很差,但求解QP的一阶方法通常需要数千次迭代。此外,实时控制应用程序对求解器具有严格的延迟限制[33]。因此,开发高效的启发式算法以在更少的迭代中解决QP是很重要的。乘法器交替方向法(ADMM)[6,15,18]是一种有效的一阶优化算法,是广泛使用和最先进的算子分裂QP(OSQP)求解器[44]的基础。ADMM基于QP的最优性条件对矩阵执行线性求解以生成步长方向,然后将步长投影到约束边界上。尽管是最先进的,ADMM算法有许多超参数,这些超参数必须用启发式算法进行调整,以正则化和控制优化。最重要的是,步长参数ρ对收敛速度有相当大的影响。然而,仍不清楚在尝试QP解决方案之前如何选择ρ。虽然一些理论工作计算了最优ρ[17],但它们依赖于求解比求解QP本身困难得多的半定优化问题。或者,一些启发式算法通过在整个优化过程中调整ρ来引入“反馈”,以平衡原始残差和对偶残差[44,6,22]。