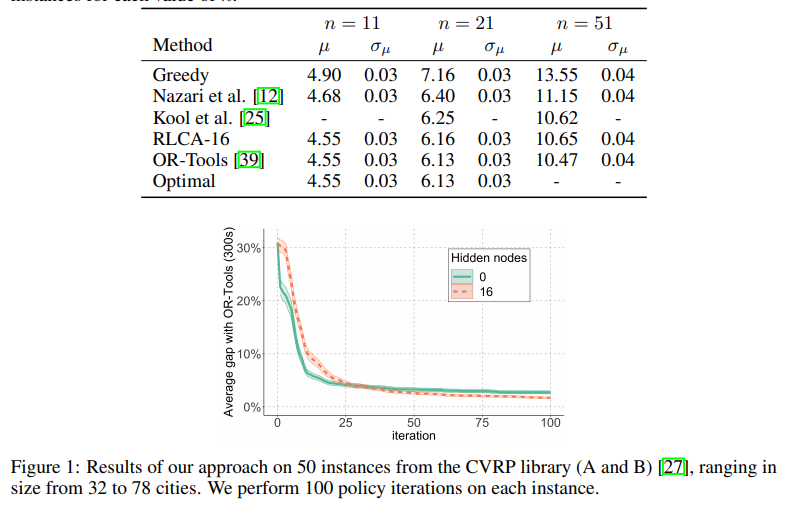
长期以来,基于价值函数的方法在强化学习中发挥了重要作用。然而,当动作空间太大而无法枚举时,在给定任意复杂度的值函数的情况下,找到最佳下一个动作是非常重要的。我们开发了一个具有组合动作空间的基于值函数的深度强化学习框架,其中动作选择问题被明确表示为混合整数优化问题。作为一个激励性的例子,我们将该框架应用于容量受限车辆路径问题(CVRP),这是一个组合优化问题,其中一组位置必须由具有有限容量的单个车辆覆盖。在每种情况下,我们将一个动作建模为单个路由的构造,并考虑通过简单的策略迭代算法改进的确定性策略。我们的方法与其他强化学习方法具有竞争力,在中等规模的标准库实例上,与最先进的OR方法相比,平均差距为1.7%。

强化学习(RL)是一种强大的工具,在解决难题方面取得了重大进展。例如,在《雅达利》[1]或《围棋》[2]等游戏中,RL算法设计出的策略远远超过了专家的表现,即使对问题结构知之甚少甚至一无所知。强化学习的成功已经推广到其他应用,如机器人[3]和推荐系统[4]。由于RL算法涵盖了越来越多的应用领域,因此需要对其进行调整和扩展,以适应新的特定问题特征。RL尚未取得令人信服的突破的一个领域是组合优化。近年来,人们做出了重大努力,将RL框架应用于NP难组合优化问题[5,6,7],包括旅行商问题(TSP)或更一般的车辆路径问题(VRP)(最近的调查见[8])。解决这些问题会对许多行业产生实际影响,包括交通、金融和能源。然而,与[1,2]相反,RL方法尚未与该领域的专家实现的性能相匹配,例如最先进的协和式TSP求解器[9,10]。设计用于组合优化的RL框架的一个主要困难是制定动作空间。基于值的RL算法通常需要足够小的动作空间来枚举,而基于策略的算法设计时考虑了连续的动作空间[11]。这两个要求严重限制了动作空间的表现力,从而将问题的全部重量放在了机器学习模型上。例如,在[12]中,选定的行动空间模型一次推进当前车辆一个城市。因此,用于组合优化的RL算法必须依赖于复杂的架构,如指针网络[5、6、12]或图嵌入[7]。本文提出了一种不同的方法,其中组合复杂性不仅由学习模型捕获,而且由底层决策问题的公式捕获。我们将重点放在容量车辆路径问题上,这是运筹学中的一个经典组合问题[13],其中一辆容量有限的车辆必须被分配一条或多条路径,以满足客户需求,同时最小化总行驶距离。尽管CVRP与TSP有着密切的关系,但它是一个更具挑战性的问题,而且最佳方法无法跨越数百个城市。我们的方法是将其表述为一个顺序决策问题,其中状态空间是一组未访问的城市,行动空间由可行路径组成。我们使用一个小的神经网络来估计一个状态的价值函数(即其运行成本)。然后,行动选择问题本身是组合的,其结构为带有背包约束和未访问城市的非线性成本的有奖旅行推销员问题(PC-TSP)。至关重要的是,PC-TSP是一个比CVRP简单得多的组合问题,使我们能够轻松地利用问题的一些组合结构。