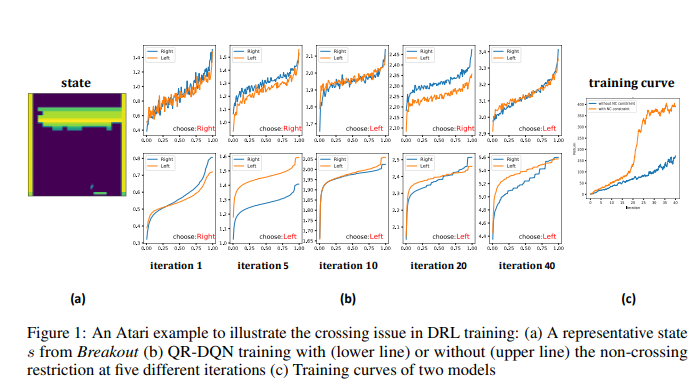
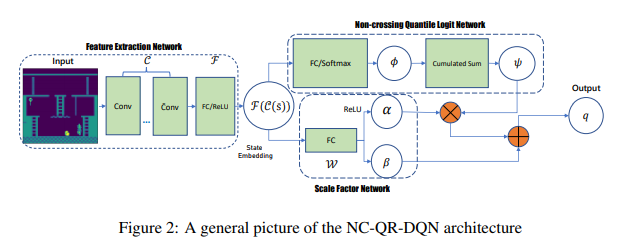
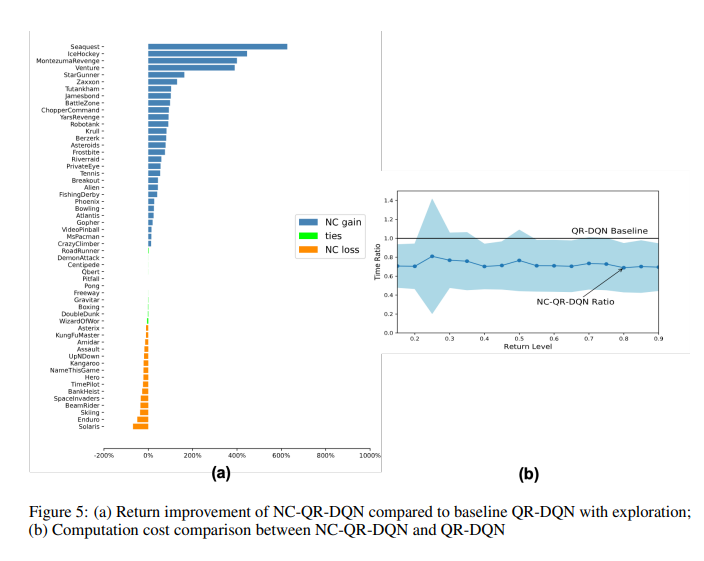
分布强化学习(DRL)估计未来收益的分布,而不是平均值,以更有效地捕捉MDP的内在不确定性。然而,基于批处理的DRL算法无法保证学习分位数曲线的非递减特性,尤其是在早期训练阶段,这导致异常分布估计和模型可解释性降低。为了解决这些问题,我们引入了一个通用的DRL框架,通过使用非交叉分位数回归来确保每个采样批次内的单调性约束,该框架可以与一些著名的DRL算法相结合。我们从理论和模型实现的角度证明了我们方法的有效性。Atari 2600 Games上的实验表明,一些具有非交叉修改的最新DRL算法在更快的收敛速度和更好的测试性能方面可以显著优于基线。特别是,当奖励空间非常稀疏时,我们的方法可以有效地恢复分布信息,从而显著提高探索效率。

与完全关注预期未来回报的基于价值的强化学习算法[16,21,22]不同,分布强化学习(DRL)[12,20,24,17,1]还通过将总回报建模为随机变量来解释马尔可夫决策过程[5,4,19]中的内在随机性。现有的DRL算法分为两大类,其中一类学习一组预定义位置的分位数值,如C51[1]、Rainbow[10]和QR-DQN[5]。放松对值范围的限制使QR-DQN比C51和Rainbow有了显著的改进。最近的一项研究,由[4]提出的IQN,将注意力从估计离散的分位数集合转移到了分位数函数。IQN具有比QR-DQN更灵活的架构,允许从均匀分布中采样分位数分数。有了足够的网络容量和无限数量的分位数,IQN理论上可以近似于完全分布。分布RL方法的一大挑战是如何评估学习的分位数分布的有效性。在多个百分位数处拟合分位数回归的一个常见问题是所获得的分位数估计的非单调性。这个问题的很大一部分可以归因于这样一个事实,即分位数函数是在不同的分位数水平上单独估计的,而不应用任何全局约束来确保单调性。有限的训练样本显著增强了交叉现象,尤其是在训练过程的早期,这也增加了模型解释的难度。如果没有不交叉的保证,策略搜索的方向可能会被扭曲,并且最佳行动的选择在不同的训练时期会有很大的差异。另一方面,当使用左截断方差作为勘探奖金时,分布方差的结果估计偏差大大降低了勘探效率[15]。有时,在检查某些风险偏好政策时,上分位数而不是平均值(Q值)具有特殊意义。由于分位数的异常排名,交叉问题将导致尴尬的解释。尽管交叉问题已被统计学会广泛研究[13,9,14,8,6,3,2,7],但不存在用于估计一般非线性分位数分布的最优解。在本文中,我们介绍了一种在DRL框架内获得非交叉分位数估计的新方法。我们首先给出了具有单调约束的Wasserstein极小化的一个形式化定义,并在实践中探索了它和分布Bellman算子的结合。然后,我们通过在一些最先进的DRL基线上使用非交叉分位数回归来描述我们的方法的详细实现过程。通过与QR-DQN基线进行比较,我们检查了所提出的非交叉方法在Atari 2600游戏中的性能。我们重复[15]中的探索实验,以更清楚地证明我们的方法在近似真实分布和实现更准确的方差估计方面的优势。