PPO的强化学习如何实现多维度的动作呢,比如我的action是5维,是Actor根据state输出一个正态分布采样5个值作为action,还是输出5个均值和方差,从而生成5个分布来采样5个值呢? 还有如果用pytorch实现的话,哪个命令是和tf.distributions.normal效果一样的呢?
本文以连续性动作空间为例子分析,
对于连续性和非连续性的区别在于使用torch不同的distribution
一般的,连续性使用Normal 类的, 非连续性使用Categorical 类型的,
无非就是神经网络最后一层使用的是基于softmax的概率分布,还是基于比如tanh还是relu的
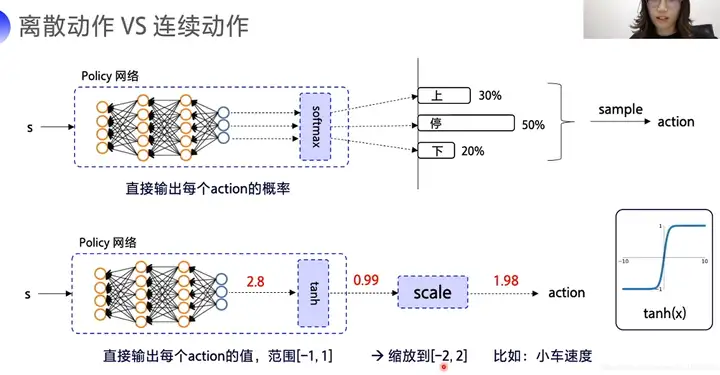
离散动作&连续动作,参考[4]
第一步: 对于一维度的分布来说,正态分布表示为:

它的图形可以表示为:
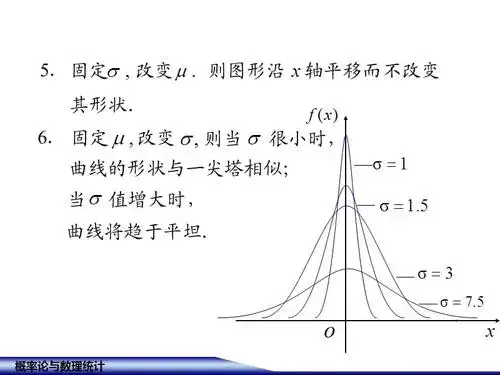
正态分布,参考[2]
对应的在torch里面可以这样实现:
import torch
from torch.distributions import Normal
means = torch.tensor([[0.0538]])
stds = torch.tensor([[0.7865]])
dist = Normal(means, stds)
action =dist.sample()
print(action)
# tensor([[-0.2358]])
第二步: 下面我们继续看提问的:action是5维的话怎么处理?
同样的道理,这时候就变成了一个多元正态分布,即多维数据的正态分布,其概率密度函数为:
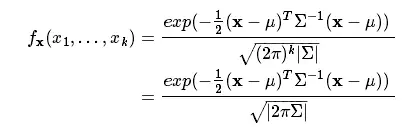
其中 x 服从 k 元正态分布,x 为 k 维向量;|Σ| 代表协方差矩阵的行列式, 它的图像表示为:
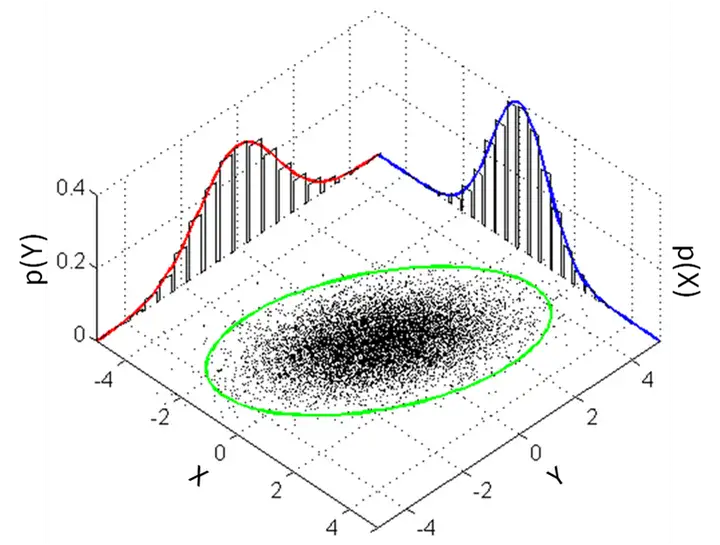
多元正态分布
可以看一下Torch文档:
具体实现表示为:
import torch
from torch.distributions import MultivariateNormal
means = torch.zeros(5)
stds = torch.eye(5)
print("means: ",means)
print("stds: ",stds)
dist = MultivariateNormal(means, stds)
action =dist.sample()
print("action: ",action)
"""
Result:
means: tensor([0., 0., 0., 0., 0.])
stds: tensor([[1., 0., 0., 0., 0.],
[0., 1., 0., 0., 0.],
[0., 0., 1., 0., 0.],
[0., 0., 0., 1., 0.],
[0., 0., 0., 0., 1.]])
action: tensor([-1.4557, -1.4514, 0.7863, 0.3571, -0.2956])
"""
第三步:在神经网络中output
class Policy(nn.Module):
def __init__(self, in_dim, n_hidden_1, n_hidden_2, num_outputs):
super(Policy, self).__init__()
self.layer = nn.Sequential(
nn.Linear(in_dim, n_hidden_1),
nn.ReLU(True),
nn.Linear(n_hidden_1, n_hidden_2),
nn.ReLU(True),
nn.Linear(n_hidden_2, num_outputs)
)
class Normal(nn.Module):
def __init__(self, num_outputs):
super().__init__()
self.stds = nn.Parameter(torch.zeros(num_outputs))
def forward(self, x):
dist = torch.distributions.Normal(loc=x, scale=self.stds.exp())
action = dist.sample()
return action
if __name__ == '__main__':
policy = Policy(4,20,20,5)
normal = Normal(5)
observation = torch.Tensor(4)
action = normal.forward(policy.layer( observation))
print("action: ",action)
参考内容:
[1]. 正态分布_百度百科
[2]. https://math.cnu.edu.cn/docs/20170327183616843684.pdf
[3]. https://pytorch.org/docs/stable/distributions.html#multinomial
[4]. https://blog.csdn.net/weixin_41