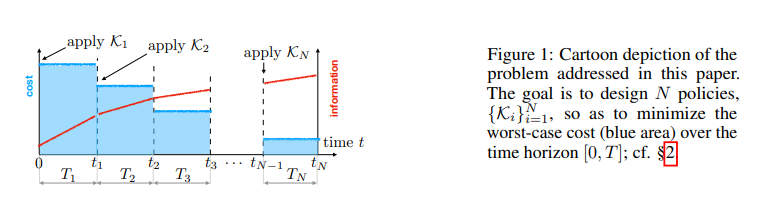
研究一类未知线性动力系统的学习控制策略问题,以使二次成本函数最小化。我们提出了一种基于凸优化的方法,可以稳健地完成这项任务:即,在给定观测数据的情况下,考虑到系统的不确定性,使最坏情况下的成本最小化。该方法平衡了开发和探索,以这样一种方式激励系统,以减少模型参数的不确定性,其中最坏情况下的成本最为敏感。数值模拟和在半实物伺服机构中的应用证明了该方法,与在两种方法中观察到的替代方法相比,具有明显的性能和鲁棒性增益。

学习在不确定和动态的环境中做出决策在许多领域都是一项至关重要的任务。尽管自20世纪60年代提出“双重控制问题”以来,强化学习(RL)一直是研究活动的主题[17],但最近的成功,尤其是在游戏中[33,37],激发了人们对该主题的兴趣。这种性质的问题需要就两个目标作出决定。首先,有一个要实现的目标,通常被量化为要最大化的奖励函数。其次,由于固有的不确定性,需要收集有关环境的信息,通常称为通过“探索”进行的“学习”。这两个目标通常是相互竞争的,这一事实被称为RL中的勘探/开发权衡,以及控制中的“双重效应”(决策)。重要的是要认识到,第二个目标(探索)只有在促进第一个目标(最大化回报)的情况下才重要;降低不确定性没有内在价值。因此,勘探应具有针对性或针对具体应用;它不应该任意地激励系统,而是以这样一种方式,即收集的信息对于实现目标是有用的。此外,在许多真实世界的应用中,希望探索不会损害系统的安全和可靠操作。本文研究不确定线性动力系统的控制,其目标是最大化(最小化)作为状态和行为的二次函数的报酬(成本);有关详细的问题公式,请参见§2。我们推导了通过执行稳健、有针对性的勘探来平衡勘探/开采权衡的综合控制策略的方法:稳健的意义是,考虑到我们对系统知识的不确定性,我们对最坏情况下的性能进行了优化,从政策激励系统的意义上讲,有针对性,以减少不确定性,从而使最坏情况下的成本最小化。为此,本文做出了以下具体贡献。我们导出了系统参数估计误差谱范数的高概率界,其形式适用于鲁棒控制综合和目标探测设计;参见§3。我们还导出了最坏情况(w.r.t.参数不确定性)无限水平线性二次调节器(LQR)问题的凸近似;参见§4.2。然后,我们将这两个发展结合起来,通过凸半定规划(SDP),给出了不确定线性动力系统的最坏情况二次成本最小化问题的近似解;参见§4。为简明起见,我们将其称为“稳健强化学习”(RRL)问题。