虽然深度强化学习(RL)在机器学习方面取得了多次引人瞩目的成功,但由于它的数据效率往往较差和它所产生的策略的通用性有限,因此阻碍了更广泛的采用。减轻这些限制的一个有希望的方法是将更好的RL算法的开发转换为一个机器学习问题本身,在一个称为meta-RL的过程中。Meta-RL最常在问题设置中进行研究,在给定任务分布时,目标是学习一种能够用尽可能少的数据从任务分布中适应任何新任务的策略。
本文由牛津大学和斯坦福大学联合推出,详细描述了元rl问题的设置以及它的主要变化。坐着将讨论如何在高水平上,基于任务分布的存在和每个单独任务的学习预算进行聚类。使用这些集群,调查元rl算法和应用程序。最后,介绍了在为深度RL从业者制作元RL作为标准工具箱的一部分的路径上的开放问题。

元强化学习(meta-RL)是一类机器学习(ML)方法,用来学习强化学习。也就是说,meta-RL使用样本低效的ML来学习样本高效的RL算法或其组件。因此,元RL是元学习的一种特殊情况,具有学习算法是RL算法的性质。Meta-RL已经被研究为一个机器学习问题的重要一段时间。有趣的是,研究也显示了大脑中元rl的类似物。Meta-RL有潜力克服现有的人类设计的RL算法的一些限制。虽然在过去的几年里,深度RL已经取得了显著的进展,但也有一些成功的故事,如掌握了Go 的游戏,平流层气球导航,或在具有挑战性的地形中的机器人运动。RL仍然非常低,这限制了其现实世界的应用。Meta-RL可以产生比现有的RL方法)的RL算法更有效的样本,甚至为以前棘手的问题提供解决方案。
元-rl算法的性能是根据任务分布中任务M的内环策略πφ所获得的回报来衡量的。根据应用程序的不同,所考虑的目标会略有不同。对于某些应用程序,我们可以提供一个老化或适应期,在此期间,只要内环找到的最终策略解决了任务,内环产生的策略的性能并不重要。在这个老化阶段的情节可以被内环用来自由地探索任务。对于其他应用程序,老化周期是不可能的,相应地,代理必须最大化它与环境交互的第一个时间步长的预期回报。最大限度地实现这些不同的目标会导致不同的学习性探索策略:当风险实现时,老化可以以浪费培训资源为代价来实现更多的风险承担。在形式上,这两种设置的元rl目标都是:
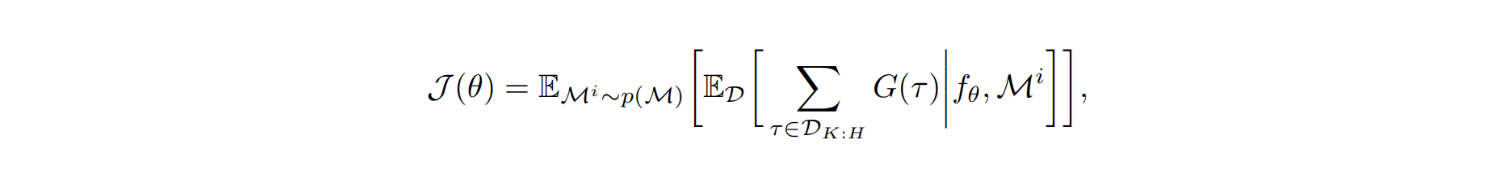
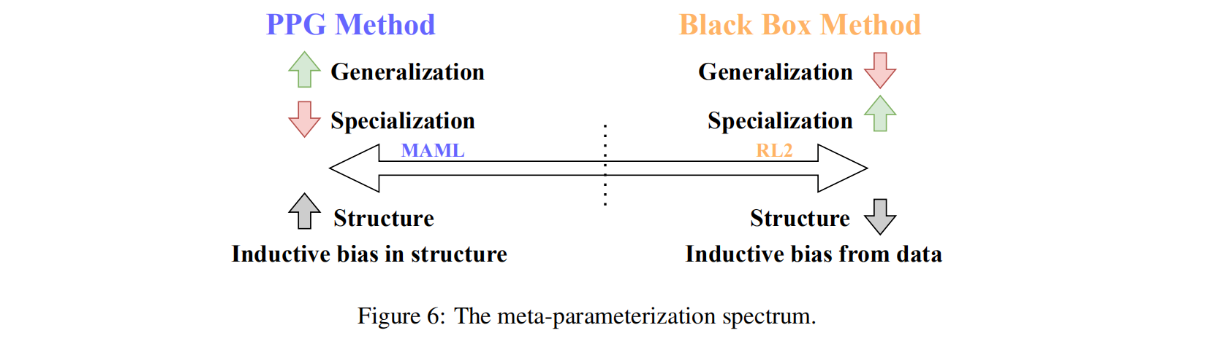
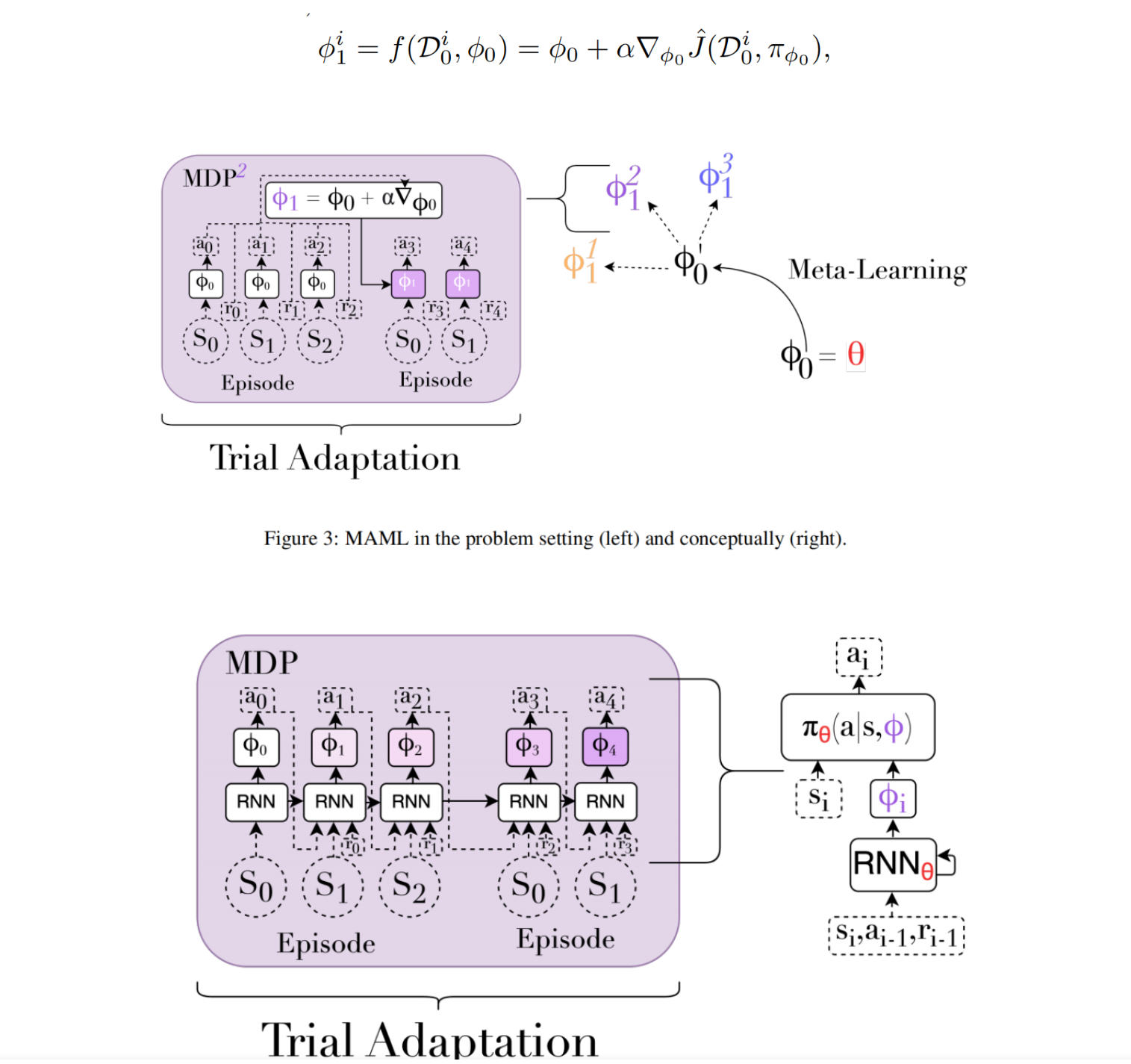
MAML内环算法fθ的许多设计都建立在现有的RL算法之上,并使用元学习来改进它们。MAML 是一个遵循这种模式的有影响力的设计。它的内环是一种策略梯度算法,其初始参数为元参数φ0 = θ。关键的观点是,这种内环是初始参数的可微函数,因此初始化可以通过梯度下降进行优化,从而成为从任务分布中学习任务的良好起点。当适应新任务时,MAML使用初始策略收集数据,并通过对任务应用策略梯度步骤来计算一组更新的参数
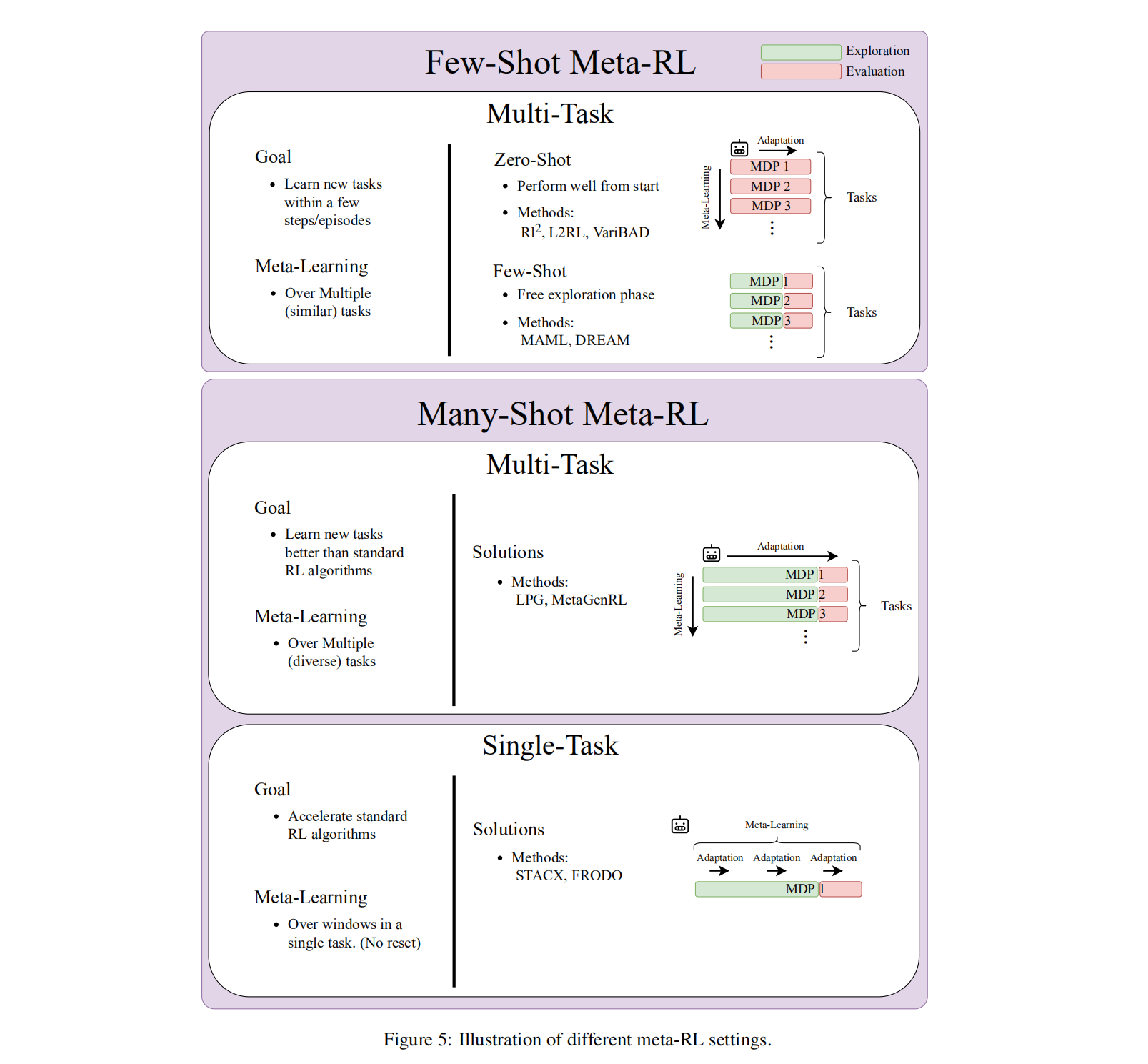
Few-Shot Meta-RL
元rl本身学习了一个学习算法fθ。这对fθ提出了独特的要求,并为这个函数提出了特定的表示。作者将这种设计选择称为元参数化,最常见的方法如下: