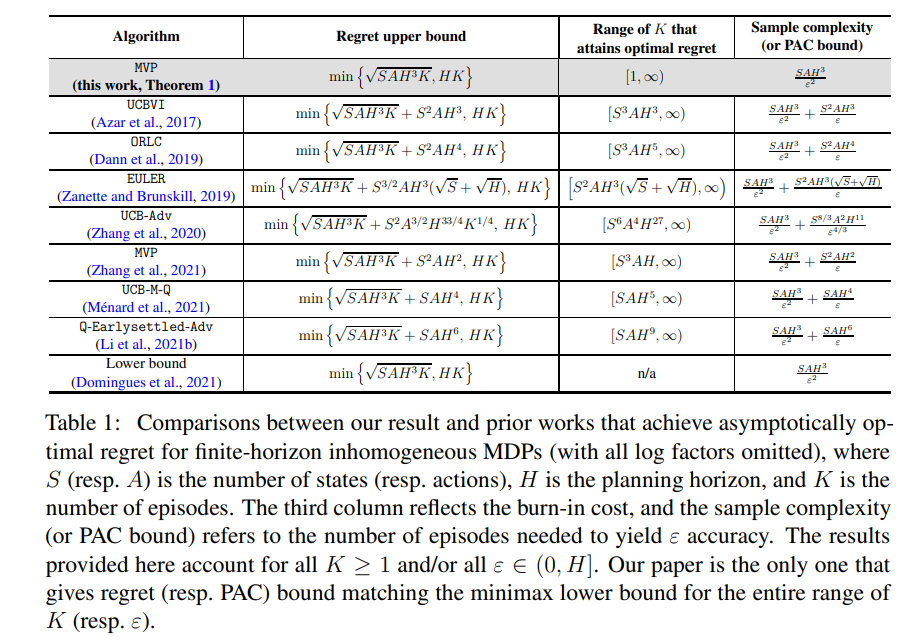
在线强化学习(RL)的核心问题是数据效率。 虽然最近的一些工作在在线强化学习中实现了渐近最小遗憾,但这些结果的最优性只能在“大样本”状态下才能保证,为了使算法能够最佳运行,需要付出巨大的老化成本。 如何在不产生任何老化成本的情况下实现最小最大最优后悔一直是强化学习理论中的一个悬而未决的问题。 我们在有限范围非齐次马尔可夫决策过程的背景下解决了这个问题。 具体来说,我们证明了单调值传播(MVP)的修改版本,这是由Zhang等人提出的一种基于模型的算法。 (2021),实现了对(模对数因子)min √ SAH3K, HK 的顺序的遗憾,其中 S 是状态数量,A 是行动数量,H 是规划范围,K 是 总集数。 此遗憾与样本大小 K ≥ 1 的整个范围的极小极大下限相匹配,基本上消除了任何烧毁要求。 它还转换为 SAH3 ε 2 的 PAC 样本复杂性(即产生 ε 准确度所需的事件数)直至对数因子,这对于整个 ε 范围来说是极小极大最优。 此外,我们扩展了我们的理论,以揭示与问题相关的量的影响,例如最优价值/成本和某些方差。 关键的技术创新在于开发一种新的遗憾分解策略和一种新颖的分析范式,以解耦复杂的统计依赖性——这是在样本匮乏的情况下在线强化学习分析面临的长期挑战