在强化学习(RL)领域,已经分析了策略梯度(PG)的各种加速方法。然而,对PG上广泛使用的基于动量的加速方法的理论理解仍然很大。为了应对这一差距,我们将著名的Nesterov的加速梯度(NAG)方法应用于RL中的策略优化,称为加速策略梯度(APG)。为了证明APG在实现快速收敛方面的潜力,我们正式证明了在真梯度和softmax策略参数化下,APG以以下速率收敛到最优策略:(i)步长几乎恒定的O(1/t2);(ii)具有时变步长的O(e−ct)。据我们所知,这是RL背景下NAG收敛率的第一个特征。值得注意的是,我们的分析依赖于一个有趣的发现:无论参数初始化如何,APG最终都会进入一个局部近似凹形的状态,在该状态下,APG可以在有限迭代内从动量中显著受益。通过对Atari 2600基准的数值验证和实验,我们确认APG在步长几乎恒定的情况下表现出I O(1/t2)的速率,在步长随时间变化的情况下具有线性收敛速率,显著提高了标准PG的收敛性。

策略梯度(PG)是强化学习(RL)领域用于策略优化的一种基本技术。它通过直接优化RL目标来确定最优策略,采用类似于传统优化问题中梯度下降算法的一阶导数。值得注意的是,PG已经证明了实证上的成功(Mnih等人,2016;Wang等人,2016,Silver等人,2014;Lillicrap等人,2016Schul-man等人,2017;Espeholt等人,2018),并得到了强有力的理论保证的支持(Agarwal等人,2021;Fazel等人,2019;Liu等人,2020;Bhandari&Russo,2019;Mei等人,2020,Wang等人,2021,梅等人,2021a;2022;Xiao,2022;Chen&Maguluri,2022;Lan,2023)。在最近的一项研究中,Mei等人(2020)描述了非正则化表格softmax设置中PG的O(1/t)收敛率。尽管RL目标缺乏最大化的凹特性,但这种收敛行为与凸最小化问题的梯度去跟踪算法一致。此外,强化学习文献的进步引入了通过各种加速技术提高O(1/t)收敛速度的理论。Khodadadian等人(2021);肖(2022)对具有时变步长的自然政策梯度(NPG)进行了深入分析,证明了其显著的线性收敛速度。另一方面,Mei等人(2021b)利用归一化梯度来加速PG,也实现了线性收敛速度。除了上述加速技术外,动量是优化文献中另一种流行的加速方法,由于其简单性,在实践中成为加速RL策略优化的广泛采用的策略(Vieillard等人,2020;Huang等人,2020)。经典的动量方法,如Nesterov动量(Nesterov,1983)和重球方法(Polyak,1964),已经无缝集成到优化求解器和深度学习框架中,如PyTorch(Paszke等人,2019)。这些方法始终优于A2C(Konda&Tsitsiklis,1999)和PPO(Schulman等人,2017)下的标准PG方法,正如精神研究所证明的那样(Henderson等人,2018;Andrychowicz等人,2021)。Nesterov(1983)提出的加速梯度(NAG)方法是从O(1/t)的梯度下降率到O(1/t2)的一阶逼近收敛速度。尽管在过去的几十年里,NAG在各种类型的优化问题中具有广泛的适用性,但据我们所知,NAG的收敛速度从未在RL的背景下进行过理论分析,这主要是由于RL目标的非凹性。因此,存在一个重要但尚未探索的研究问题:在RL的背景下,Nesterov动量能否实现比现有PG和其他加速方法更好或可比的收敛速度?为了回答这个问题,本文引入了加速策略梯度(APG),它利用Nesterov加速来解决RL的策略优化问题。尽管之前的研究中已有关于NAG方法的知识(Beck&Teboulle,2009a;b;Ghadimi&Lan,2016;Li&Lin,2015;Su等人,2014;Carmon等人,2018),
在RL领域内建立收敛率仍然存在几个基本挑战:
(i) 非凸问题下的NAG收敛结果:尽管有大量的理论工作研究了一般非凸问题上NAG的收敛性,但这些结果只建立了一阶最优性测度的收敛性。仅根据这些结果来表征收敛速度是不可行的。
(ii)动量项的固有特征:从分析的角度来看,动量项表明了与先前更新的复杂相互作用。因此,准确量化APG执行过程中动量的具体影响是一个相当大的挑战。
(iii)softmax参数化下无界最优参数的性质:在优化理论中表征次优差距的一个关键因素是初始参数和最优参数之间距离的范数(Beck&Teboulle,2009a;b;Ghadimi&Lan,2016)。然而,在RL中的softmax参数化的情况下,每个状态的最优动作的参数趋于无穷大。因此,次优间隙中涉及的范数变得无限,从而阻碍了使用现有结果来表征收敛速度。我们的贡献。尽管存在上述挑战,我们对上述研究问题给出了肯定的答案,并首次描述了RL背景下NAG收敛速度的特征。
具体而言,我们提出了解决上述技术挑战的有用见解和新技术:关于(i),我们发现了RL目标的一个基本属性,称为局部近凹性,这表明RL目标在最优策略附近几乎是凹性的,尽管其全局景观是非凹性的。对于(ii),我们表明局部近凹区域是吸收的,因为即使有动量项的影响,政策参数一旦进入,肯定会留在近凹区域。
这一结果是通过仔细量化每个动量项的累积效应而获得的。针对(iii),我们引入了具有有界范数并诱导近似最优策略的替代最优参数,从而表征了APG的收敛速度。
我们将本文的贡献总结如下:
•我们引入了APG,它利用Nesterov momen-tum方案来加速RL的PG收敛性能。据我们所知,这是在RL背景下理解Nesterov动量收敛的第一次正式尝试。
•为了证明APG在实现快速收敛方面的潜力,我们正式确定APG在具有几乎恒定步长的softmax策略参数下具有I O(1/t2)的收敛率。
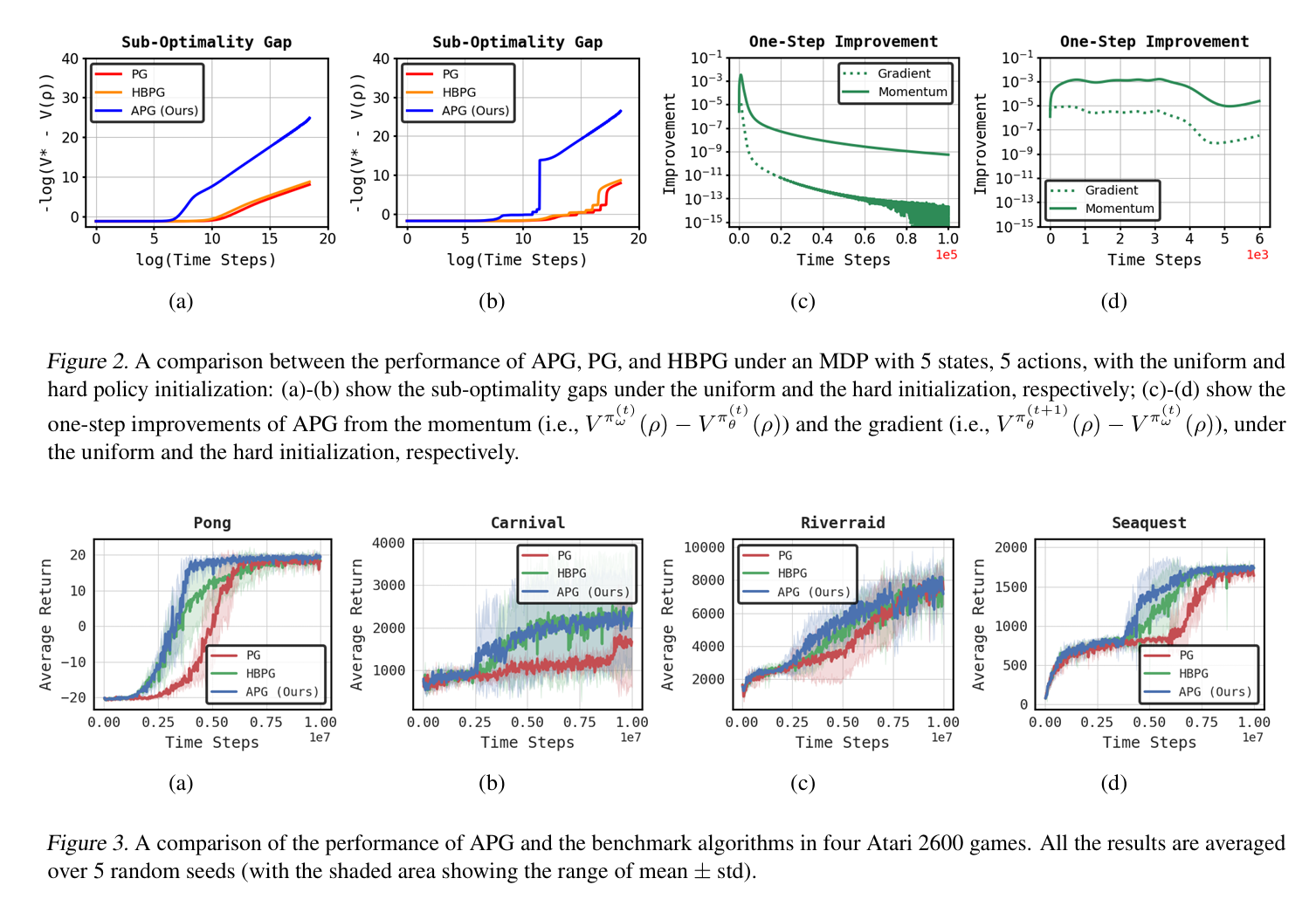
此外,我们提出,如果允许时变步长,APG也可以实现O(e-ct)的线性收敛率。这些方法在恒定步长和时变步长的情况下都能提供更好或可比的结果。为便于参考,表1中给出了总结比较。为了实现这一目标,我们提出了对RL和APG的几个新见解,包括局部近凹特性以及APG的吸收行为。此外,我们还表明,这些性质也可以应用于建立PG的O(1/t)收敛率,这具有独立的意义通过对MDP问题的数值验证,我们发现APG在步长几乎恒定的情况下表现出I O(1/t2)的速率,在步长随时间变化的情况下具有线性收敛速率,从而大大改善了标准PG的收敛行为。此外,我们在基准Atari游戏上验证了我们的APG算法,并证明了Nesterov动量提供的显著优势。