标题:非平稳多智能体强化学习的黑箱方法
A BLACK-BOX APPROACH FOR NON-STATIONARY MULTI-AGENT REINFORCEMENT LEARNING

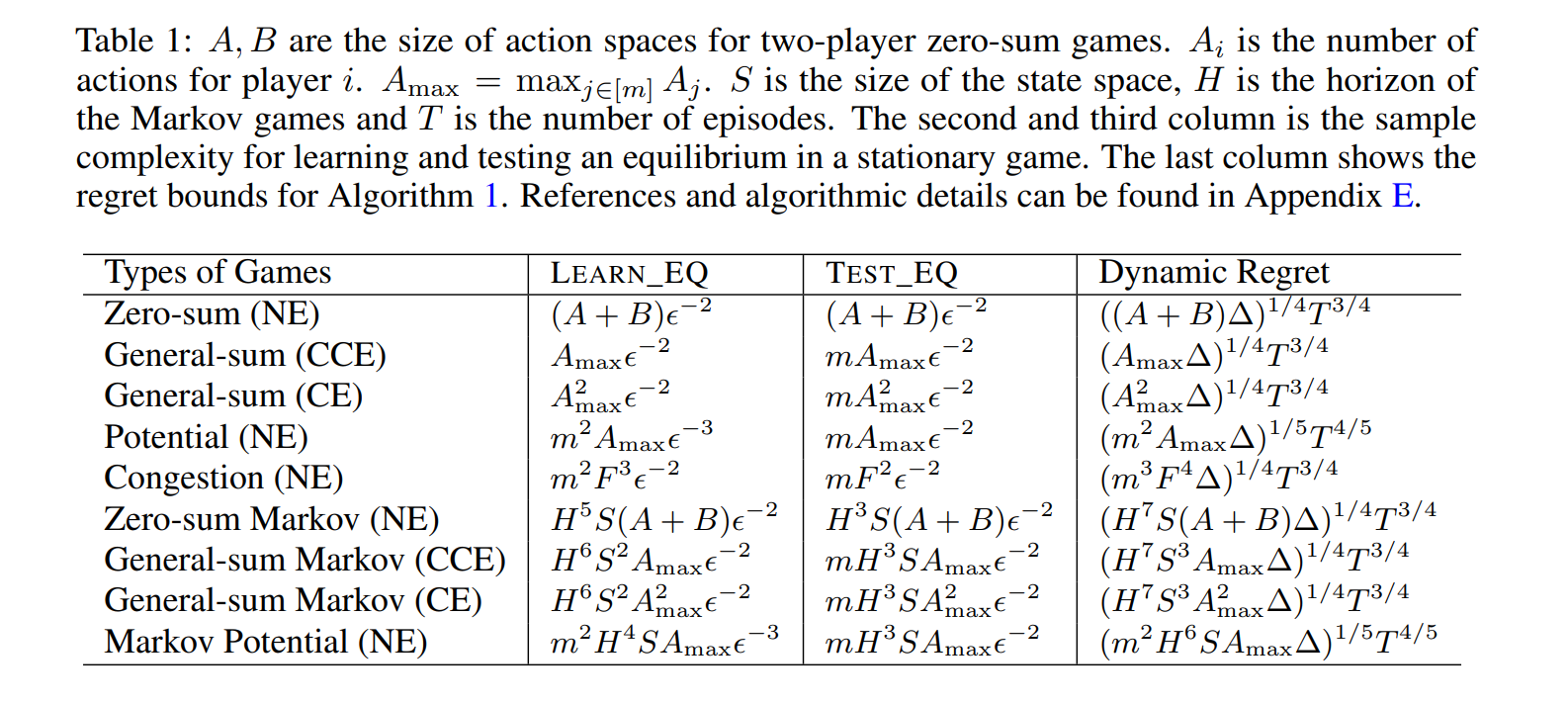
本文研究了非平稳多智能体系统中的均衡学习问题,并解决了将多智能体学习与单智能体学习区分开来的挑战。特别是,我们关注于具有bandit反馈的游戏,其中测试一个均衡可能会产生显著的遗憾,即使要测试的差距很小,以及在平稳游戏中存在多个最优解(均衡)所带来的额外挑战。为了克服这些障碍,我们提出了一种适用于多种问题的通用黑盒方法,如一般和博弈、势博弈和马尔可夫博弈,只要为平稳环境配备了适当的学习和测试oracle。当非平稳度(通过总变化量∆衡量)已知时,我们的算法可以实现O(∆1/4T3/4)的遗憾,当∆未知时,遗憾为O(∆1/5T4/5),其中T是轮次数。同时,我们的算法继承了oracle对智能体数量的有利依赖。作为可能独立感兴趣的辅助贡献,我们展示了如何通过黑盒归约到单智能体学习来测试各种类型的均衡,包括纳什均衡、相关均衡和粗相关均衡。
Introduction
多智能体强化学习(MARL)研究多个智能体在未知环境中的相互作用,目的是最大化其长期回报(Zhang等人,2021)。该领域在多个领域都有应用,如电脑游戏(Vinyals等人,2019)、机器人技术(de Witt等人,2020)和智能制造(Kim等人,2020年)。尽管已经为MARL开发了各种算法,但通常假设潜在的重复博弈在整个学习过程中是平稳的。然而,这种假设往往无法代表环境在整个学习过程中不断演变的现实世界场景。非平稳多智能体系统内的学习任务虽然至关重要,但当试图推广非平稳单智能体强化学习(RL)时,尤其是对于向智能体透露最少信息的土匪反馈情况,会带来额外的挑战(Anagnostides等人,2023)。此外,各种多智能体设置,如零和、势和一般求和博弈,以及范式和扩展型博弈,以及完全可观察或部分可观察的马尔可夫博弈,进一步使专门算法的设计复杂化。在这项工作中,我们迈出了理解具有土匪反馈的非平稳MARL的第一步。首先,我们指出了区分非平稳MARL和非平稳单代理RL,以及区分土匪反馈和全信息反馈的几个挑战。随后,我们提出了在任意非平稳游戏中具有亚线性动态遗憾的黑盒算法,前提是在相应的(近)平稳环境中可以获得学习算法。这种多功能的方法使我们能够利用现有的算法进行各种固定游戏,同时促进对未来算法的无缝适应,从而提供更好的保证
研究背景与动机:
- 多智能体强化学习(MARL):研究多个智能体在未知环境中的交互,旨在最大化其长期回报。
- 非平稳环境:现实世界中环境常常是非平稳的,这导致传统假设平稳环境的MARL算法不适用。
- bandit反馈:智能体仅能获得所选动作的奖励信息,这增加了学习难度。
主要挑战:
梯度估计困难:bandit反馈下,奖励梯度难以估计,与基于在线学习的算法不兼容。
测试均衡的代价:测试任意小的均衡差距可能产生O(1)的遗憾。
均衡的非唯一性:使得基于重播的测试变得困难。
算法泛化困难:从非平稳单智能体强化学习到非平稳MARL的泛化不是直截了当的。
黑盒方法:
具体算法:
实际应用:
未来工作: