IMPACT OF COMPUTATION IN INTEGRAL REINFORCE MENT LEARNING FOR CONTINUOUS-TIME CONTROL《计算对连续控制积分强化学习的影响》
效用函数在政策评估(PEV)阶段的积分。这是通过正交规则实现的,正交规则是从离散时间获得的状态样本中评估的效用函数的加权和。我们的研究揭示了一个关键但尚未被充分探索的现象:计算方法的选择——在这种情况下是求积规则——会显著影响控制性能。这种影响可以追溯到这样一个事实,即PEV阶段引入的计算误差会影响策略迭代的收敛行为,进而影响学习控制器。为了阐明计算如何影响控制,我们将IntRL的策略迭代与应用于哈密顿-雅可比-贝尔曼方程的牛顿方法进行了比较。从这个角度来看,PEV中的计算误差表现为牛顿法每次迭代中的额外误差项,其上限与计算误差成正比。此外,我们证明了当效用函数位于再现核Hilbert空间(RKHS)中时,通过使用贝叶斯求积和RKHS诱导核函数可以实现最优求积。我们使用梯形规则和贝叶斯求积法证明了In-tRL的局部收敛率为O(N-2)和O(N-b),其中N是等距样本的数量,b是Mat´ern核的平滑参数。这些理论发现最终通过两个规范控制任务得到了验证。
强化学习(RL)的最新进展主要集中在离散时间(DT)系统上。著名的应用包括雅达利游戏Schrittwieser等人(2020)、Go Silver等人(2016;2017)以及大型语言模型Bubeck等人(2023)。然而,大多数物理和生物系统在时间上本质上是连续的,并由微分方程动力学驱动。这种固有的差异强调了连续时间RL(CTRL)算法进化的必要性Baird(1994);Lewis等人(1998);阿布·哈拉夫和刘易斯(2005);弗拉比和刘易斯(2009);Vrabie等人(2009);Lewis&Vrabie(2009);Vamvoudakis&Lewis(2010);Modares等人(2014);李等(2014);莫达雷斯和刘易斯(2014);Vamvoudakis等人(2014);Yildiz等人(2021);霍尔特等人(2023);华莱士与斯(2023)。不幸的是,采用CTRL既带来了概念上的挑战,也带来了算法上的挑战。首先,已知Q函数在CT系统中消失Baird(1994);阿布·哈拉夫和刘易斯(2005);Lewis和Vrabie(2009),这使得即使是简单的RL算法,如Q学习,也不适用于CT系统。其次,DT系统中的一步过渡模型需要用时间导数代替,这导致CT-Bellman方程(也称为非线性李雅普诺夫方程或广义哈密顿-雅可比-贝尔曼方程)由复偏微分方程(PDE)控制,而不是像DT系统Lewis&Vrabie(2009)那样由简单的代数方程(AE)控制;弗拉比和刘易斯(2009);Vamvoudakis&Lewis(2010):
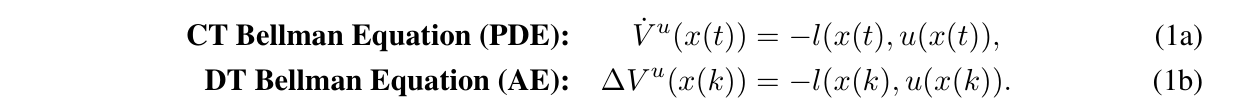
在(1a)和(1b)中,符号x、u、l、V分别表示状态、控制策略、效用函数和价值函数。虽然传统的DTRL侧重于最大化“奖励函数”,但我们的工作与大多数CTRL文献一致,采用“效用函数”来表示成本或惩罚,旨在最小化其相关价值。求解贝尔曼方程是指政策评估(PEV),这是RL Sutton等人(1998)政策迭代(PI)中的重要步骤;刘易斯和弗拉比(2009)。然而,CT-Bellman方程不能直接求解,因为l(x(t),u(x(t))的显式形式取决于通常未知的状态轨迹x(t。CT Bellman方程可以公式化为Vrabie&Lewis(2009)的区间强化;Lewis&Vrabie(2009);Modares等人(2014);莫达雷斯和刘易斯(2014);瓦姆沃达基
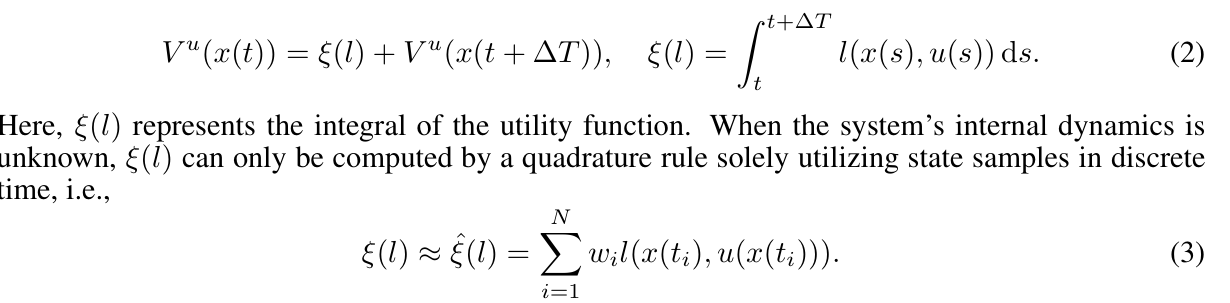
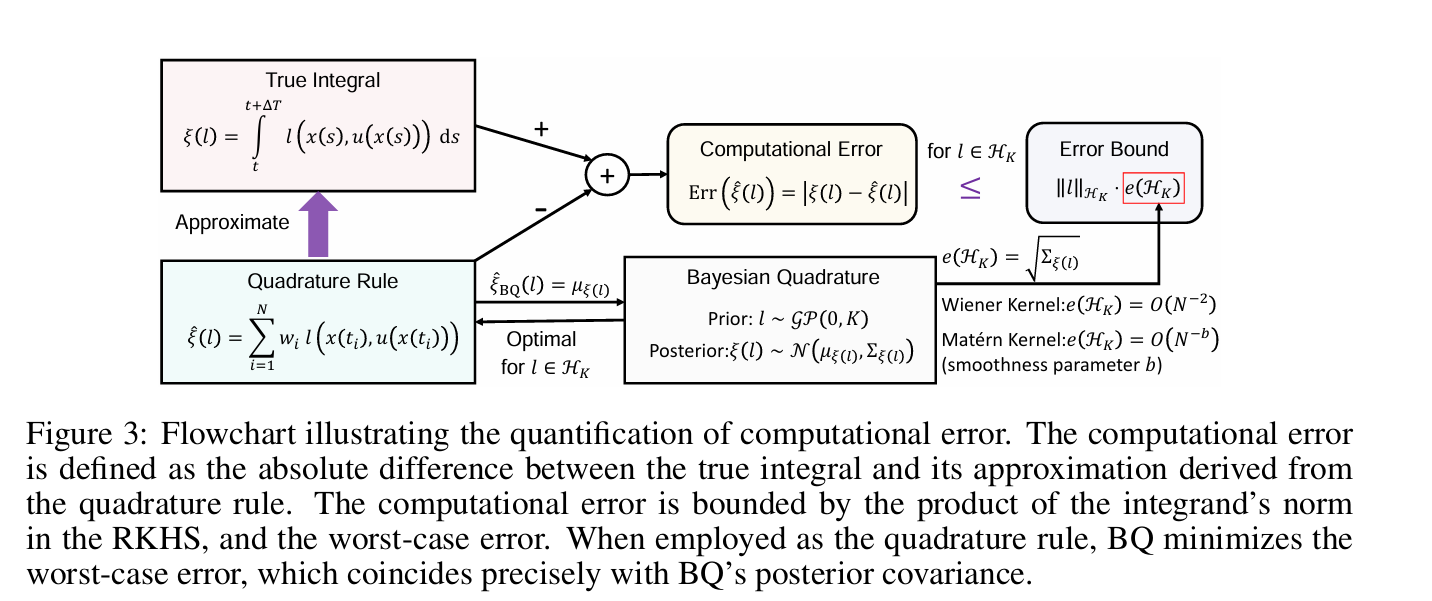
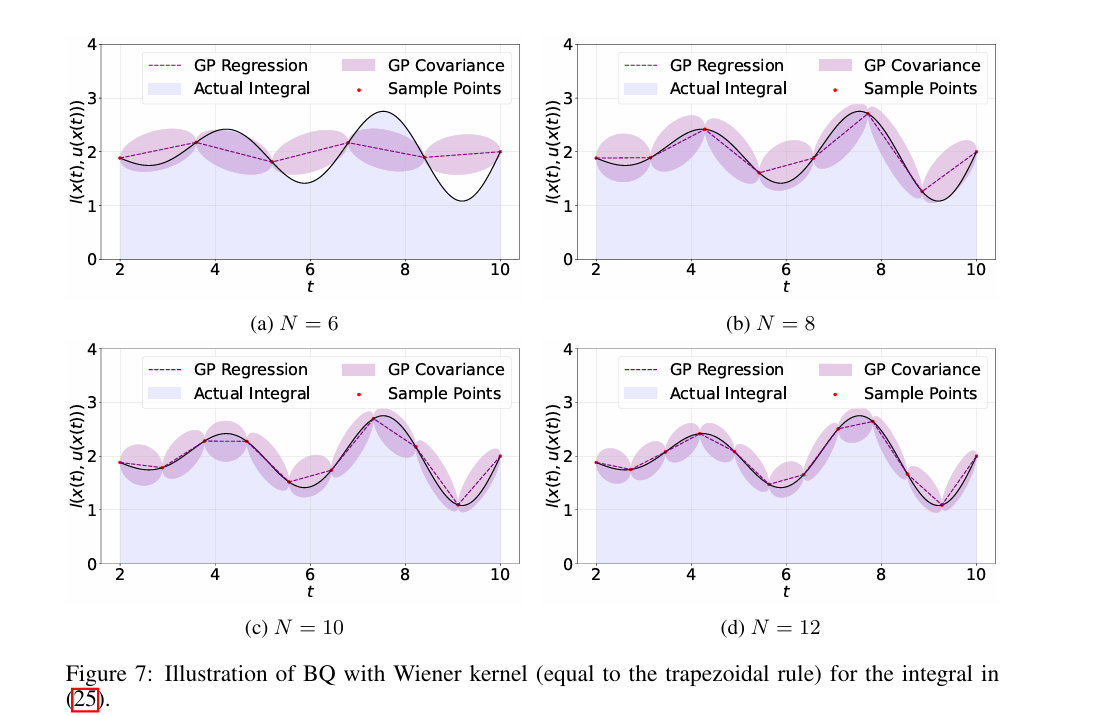
这里,收集状态样本的时刻为t1=t<t2<··<tN=t+∆t,N为样本量。正交规则的特征是一组权重{wi}Ni=1,可以从梯形规则等经典方法或贝叶斯求积(BQ)O'Hagan(1991)等高级概率方法中选择;Karvonen&S¨arkk¨a(2017);Cockayne等人(2019);Briol等人(2019);Hennig等人(2022)。为简单起见,我们将正交规则的计算误差表示为Err(ξ(l)):=|ξ(1)−ξ(l)|。在实际应用中,自主系统的传感器是状态样本的主要来源。例如,当CTRL算法训练无人机导航控制器时,从各种传感器收集状态样本。这些传感器包括用于定向的陀螺仪、用于运动检测的加速计、用于位置感知的光流传感器、用于高度测量的气压计和用于全球定位的GPS。如果这些传感器以10Hz的采样频率工作,并且(2)中的时间间隔∆T设置为1秒,我们将在该持续时间内获得N=11个状态样本。
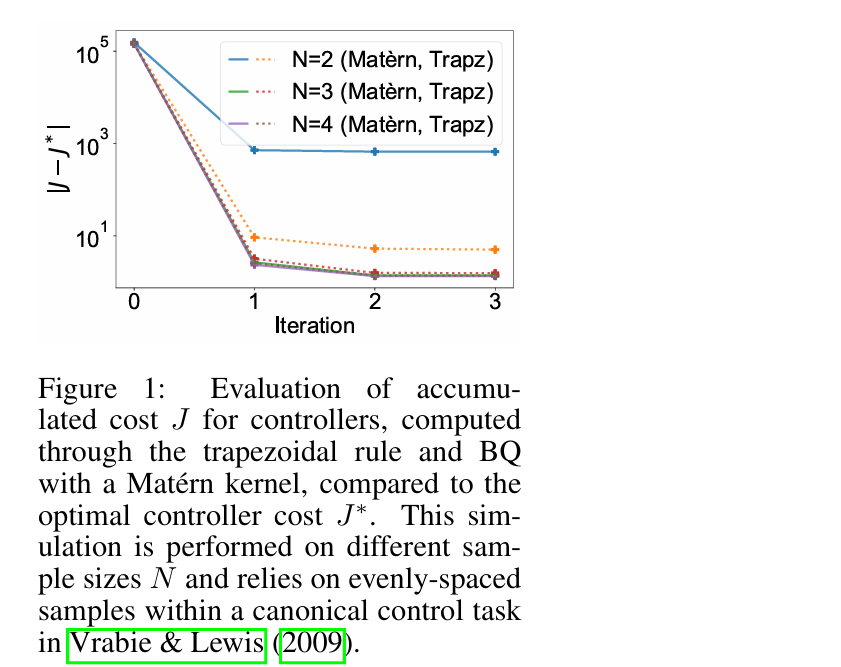
Yildiz等人(2021)强调了计算方法对CT Bellman方程解的影响。与这一发现相呼应,我们的研究进一步表明,计算方法的选择也会影响学习控制器的性能。如图1所示,我们研究了积分强化学习(IntRL)算法Vrabie和Lewis(2009)的性能。我们利用梯形规则和具有Mat´ern核的BQ来计算PEV步长,应用不同的样本量N。我们对规范控制任务的结果(Vrabie&Lewis(2009)的示例1)表明,较大的样本量会降低累积成本。此外,我们观察到这两种正交方法在累积成本方面存在显著差异。这一趋势突显了一个关键的见解:计算方法本身可能是控制性能的决定因素。这种现象不仅限于IntRL算法,而且适用于已知内部动态的CTRL算法,如附录A所述。