Policy Gradient 类的算法是深度强化学习中很重要的一类算法,也是目前最有成效的算法之一。但我在学习的过程中一直觉得这部分的知识点比较散乱,因为策略梯度类的算法包括很多种变体,经过了各种改进,初学的时候感觉就是一团乱麻,迷失在各种各样的损失函数表达式里。当看到还有 Actor-Critic 这种结构的时候更是一脸懵逼。
因此这里把这类算法做个简单的梳理,也是为了帮助自己理清思路,总结的算法包括:Reinforce,受限策略梯度,PPO1 和 PPO2。为了搞清楚具体的流程,我把三种常用算法的流程画了简图,对照流程图写程序思路更清晰。
核心设计:Policy Gradient 的损失函数
Policy Gradient 类的算法是通过梯度计算去更新策略网络的参数,因此目标函数就直接设计成期望累积奖励。这个期望值有多种表达方式,也就对应着不同的具体算法对损失函数的不同计算方法。

但因为累积奖励的期望值无法直接计算,需要采用蒙特卡洛方法,多次采样取近似的平均值。每次采样都会生成一个 Trajectory,在不断迭代运行,获取了大量的 Trajectory 后,使用一定的变换和近似去计算累积奖励,作为用于梯度更新的损失函数。
在进行梯度计算时,往往采用 log probablity 的形式,这更易于计算(在Pytorch等框架中也很容易实现)。相关近似计算的推到过程如下:
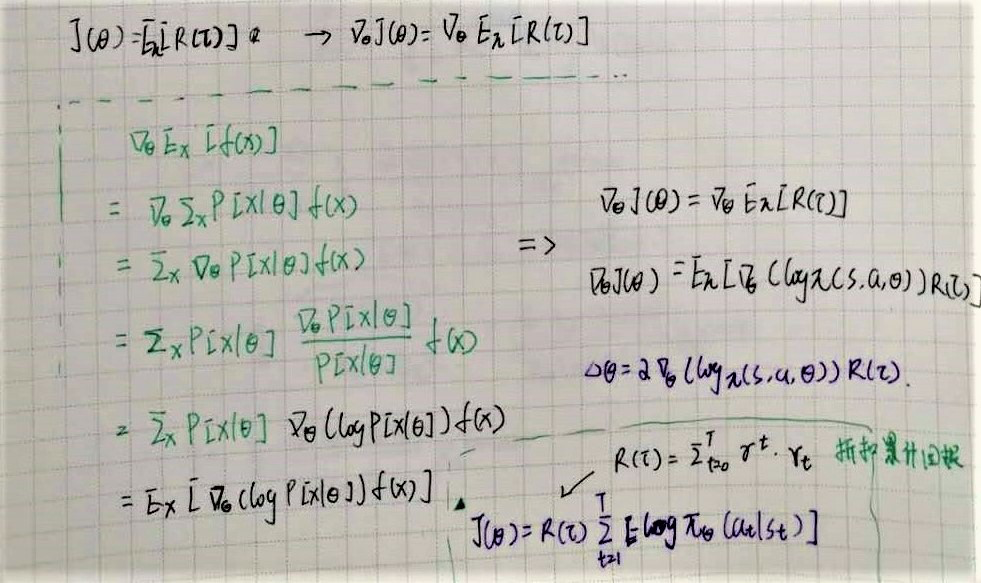
算法种类和演化:从Reinforce 到 PPO
- 原始形式 — Reinforce
最早的 Policy Gradient 算法就是蒙特卡洛策略梯度(Reinforce),基本思想就是前面说的随机采样,然后用近似的平均累积奖励去代替期望值。
把每个trajectory的累积奖励作为一个整体 R(\tau)=\sum_{t=0}^T \gamma^{t}*r_t
损失函数可以写成: J(\theta)=R(\tau) \sum_{t=1}^T [-log \pi_{\theta}(a_t|s_t)](这里的负号是为了做梯度下降,取了目标函数的负值)
- Credit Assigment
原始形式的损失函数计算了从 0-T 的所有累积奖励总和,但对于每个 time step , 当前采取的 action 只会对 >t 的时刻以后的状态产生影响,因此可以只计算未来的累积奖励,忽略过去的奖励。
对每个时间步 t,对应的未来累积奖励为: G(t)=R_t^{future}=\sum_{i=t}^{i=T} (r_i)* \gamma^{i-t}
则损失函数为 :J(\theta)=\sum_{t=1}^T [R_t^{future}(-log \pi_{\theta}(a_t|s_t))]
注意这里跟前面的不同,Reinforce 的损失函数是直接计算整个 Trajectory 的累积奖励作为一个常数,而加入了 Credit Assigment 后,是要分别对每个 time step 计算一下未来的累积奖励,然后再乘以 log probability 一起求和的。
这种在 Reinforce 的基础上做了简单改进的算法,有时也叫做受限策略梯度。蒙特卡洛策略梯度方法的特点是每次采样完一整个 Trajectory 后就更新一次策略网络的参数,如果玩 gym 等环境中的一些典型阶段性任务(CartPole,MountCar 等)的话,就是跑完一个 episode 就更新。所以这里损失函数只需要计算一个 Trajectory就可以了。
前面两种计算方法都相当于是均匀采样,而且每次跑完一个 Trajectory 就更新,是典型的随用随弃,没办法利用以往的经验。带来的潜在问题包括梯度更新的震荡过大,训练完后 agent 表现很不稳定,或者导致收敛困难等。
于是孜孜不倦的计算机大佬们就想到了另一个办法,可以类似于 DDPG 中的 Memory Buffer,对旧的经验进行循环再利用。即用以前的 old_policy 下采样得到的 trajectory ,更新当前的新 policy 参数。既然是多次采样,就需要考虑到每个 Trajectory 的采样概率不同。
当引入采样概率时,目标函数就可以写成: \sum_\tau P(\tau;\theta) f(\tau)
其中 f(\tau) 为单个 Trajactory 的目标函数, f(\tau)=\sum_{t=1}^T [R_t^{future}(-log \pi_{\theta}(a_t|s_t))]
这里有一个很管用的 Trick,就是在目标函数中引入 reweighting factor:
\sum_\tau P(\tau;\theta) f(\tau)= \sum_\tau P(\tau;\theta) \frac{P(\tau;\theta')}{P(\tau;\theta)}
(这个公式初看起来是废话,但把上面的联合概率展开以后,就会发生神奇的事情。。。)
Importance Sampling
前面两种计算方法都相当于是均匀采样,而且每次跑完一个 Trajectory 就更新,是典型的随用随弃,没办法利用以往的经验。带来的潜在问题包括梯度更新的震荡过大,训练完后 agent 表现很不稳定,或者导致收敛困难等。
于是孜孜不倦的计算机大佬们就想到了另一个办法,可以类似于 DDPG 中的 Memory Buffer,对旧的经验进行循环再利用。即用以前的 old_policy 下采样得到的 trajectory ,更新当前的新 policy 参数。既然是多次采样,就需要考虑到每个 Trajectory 的采样概率不同。
当引入采样概率时,目标函数就可以写成: \sum_\tau P(\tau;\theta) f(\tau)
其中 f(\tau) 为单个 Trajactory 的目标函数, f(\tau)=\sum_{t=1}^T [R_t^{future}(-log \pi_{\theta}(a_t|s_t))]
这里有一个很管用的 Trick,就是在目标函数中引入 reweighting factor:
\sum_\tau P(\tau;\theta) f(\tau)= \sum_\tau P(\tau;\theta) \frac{P(\tau;\theta')}{P(\tau;\theta)}
(这个公式初看起来是废话,但把上面的联合概率展开以后,就会发生神奇的事情。。。)

上面的公式称为 Surrogate Function,基本思想是利用新旧策略的比例来计算目标函数。跟直接计算 log 概率的方式相比(比如 Reinforce),可以让更新的步子更平缓,避免梯度震荡等问题。
Surrogate Function 的计算可以用两种方式,
- 一种是用上面的(未来)累积奖励,即: L_{sur}(\theta',\theta) = \sum^t[\frac{\pi_{\theta'}(a_j)}{\pi_{\theta}(a_j)}*R_t^{future}]
- 另一种是用优势函数 Advantage Function : A(t)=Q(s_t,a_t)-V(t) \approx G(t)-V(s_t)L_{sur}(\theta',\theta) = \sum^m_{j=0} [\frac{\pi_{\theta'}(a_j)}{\pi_{\theta}(a_j)}A(j)]
(注意 \theta' 和 \theta 分别代表新策略和旧策略的参数)
这也是更高级的算法,比如 PPO 计算损失函数的基础。但 Surrogate Function 存在一个问题,从前面的推到过程也能看出来,一个关键的近似计算是在新旧策略相差不大这个基础上进行的。但如果新旧策略差别较大,就会带来问题,为了考虑到这种情况,需要采取一些办法对策略更新的幅度进行限制,保证比例近似为1。这就引出了后面的 PPO。
PPO
KL 散度

KL 散度衡量了两个分布之间的差异程度,用新旧策略各自对应分布之间的 KL 散度作为惩罚项,可以对 Surrogate Function 进行约束,限制策略更新的幅度。
J(\theta) = L_{sur}(\theta',\theta) - \beta KL(\theta,\theta')
但 KL 散度在实践中较难计算,所以又衍生出了第二种 PPO 的版本。
Clipped Surrogate function
当 Policy 函数在更新过程中出现突变,Surrogate Function 对于 reward 的估计就会不准确
The big problem is that at some point we hit a cliff, where the policy changes by a large amount. From the perspective of the surrogate function, the average reward is really great. But the actually average reward is really bad!
用简单的裁剪法代替 KL 散度,也可以起到很有效的限制更新幅度的作用。

加入了 CLIP 裁剪后,Surrogate function 就可以写为:
L^{clip}{sur}(\theta^,\theta)=\sum^m_{j=0} min [( \frac{\pi_{\theta'}(a_j)}{\pi{\theta}(a_j)}A(j)),(clip_{\epsilon}(\frac{\pi_{\theta}'(a_j)}{\pi_{\theta}(a_j)})*A(j))]
这也就是第二种 PPO 算法的损失函数计算式,也是更常用的一种。