三种主要策略梯度类算法的流程对比
这里对三种常用的 Policy Gradient 类算法的流程进行了总结和对比。
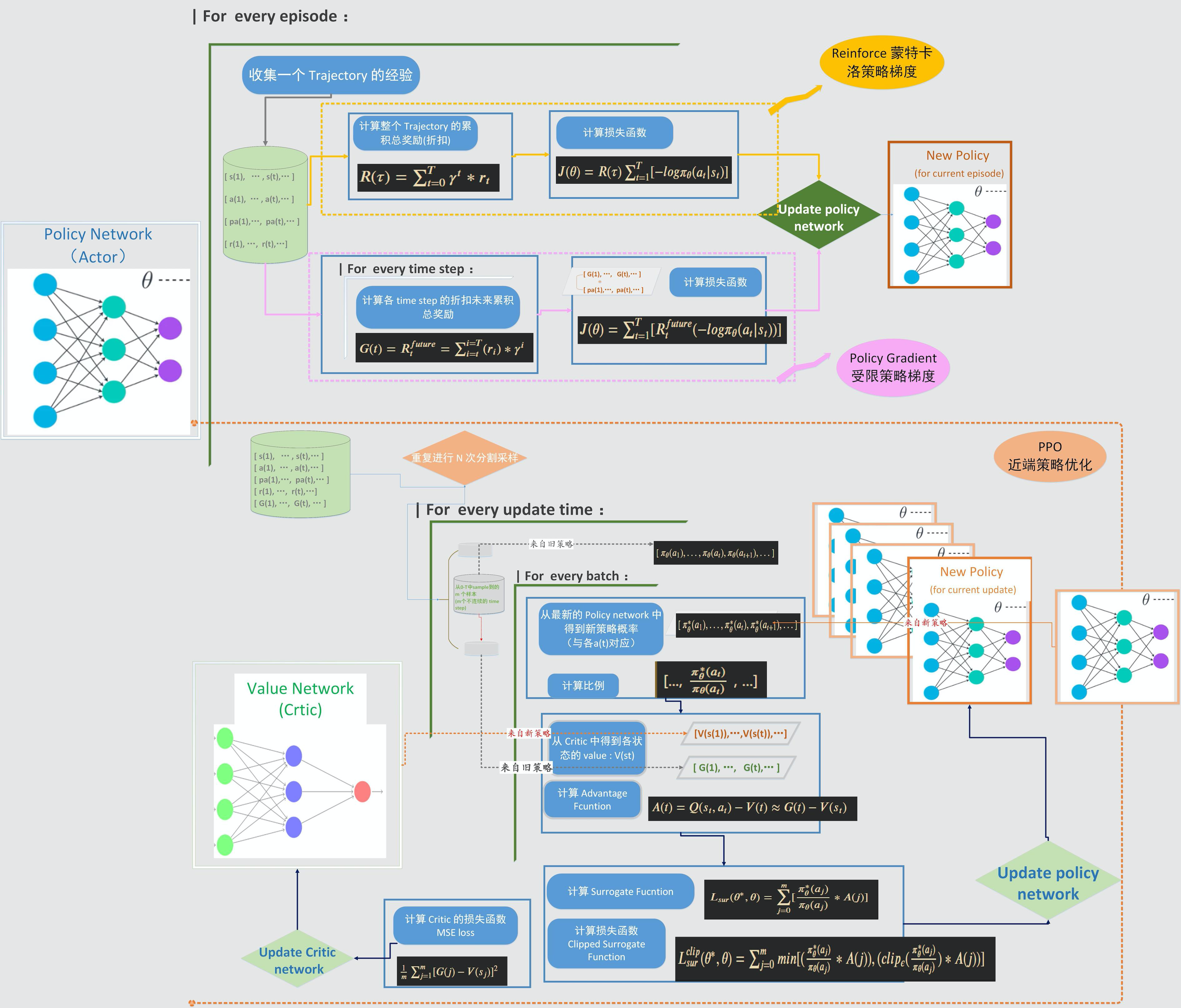
Reinforce 比较简单,受限策略梯度是在 Reinforce 的基础上对损失函数进行了改进。这两种都是每次采样完一整个 Trajectory 的数据后,再进行策略更新,属于 on policy 的更新方式。
而 PPO 则不同于前面两种,采用的是 off policy 离线策略更新。每次重复进行 N 个 Trajectory 的连续采样,然后把这些数据存入 memory buffer,更新的时候把多个 Trajectory 的样本打乱,按照 mini-batch 取用,然后进行多次迭代更新。而每次更新,策略参数就是改变,计算最新策略和旧策略(采样时的行动策略)的概率之比。而这时用于更新的策略和用于行动的策略就不是同一个了,对于一个固定的采样批次,行动策略是保持不变的,而更新的策略则在不停变化。因此是典型的离线策略更新。
如果用 Advantage 去计算损失函数,那么还需要一个 Critic 网络生成 value function , 这时 PPO 的结构就类似于 Actor-Critic,但是 Critic 输出的是 V 而不是 Q,更新相对简单。
近端策略优化算法 PPO
PPO 伪代码

算法关键点
优势函数:Actor-Critic结构 ,Advantage 的计算
直接用 A=G-V
使用 GAE 方法计算 ✳
Clipped Surrogate function ,off policy 离线策略更新
加入 entropy 项作为对 new policy 的限制 ✳
policy 更新的问题
更新的时机:跑完一个episode再更新,还是收集固定数量的 exp 就可以更新
更新的频率,更新前后两个 \pi_\theta 的差异程度,对梯度计算的影响
是否引入梯度剪裁 clip_grad_norm_
Policy Loss 的最终形式 ✳
Critic 网络更新的问题
损失函数计算: L_c = MSE(G-V)
Critic 与 Actor 同步更新,对自身损失函数的影响,是否会导致梯度不稳定
Actor 和 Critic 网络结构和超参数配置对学习的影响
PPO 在连续控制场景中的应用关键点(contiounus action space)
由于 PPO 属于随机策略 stochastic policy,网络不能直接输出连续动作的取值(与DDPG不同),而是需要输出action 的概率分布
policy 网络包含两个输出层,分别对应着动作概率分布的均值 和方差 ,每个输出层的维度与 action 的维度一致
action 的生成需要从动作概率分布中采样,既先把当前 state 输入 policy 网络,得到动作概率分布,再从中采样得
到随机动作值
Surrogate function 中 ratio 的计算 ✳
(mus, sigmas) = self.policy(states)
dists = Normal(mus, sigmas)
new_probs=dists.log_prob(actions)
ratios = torch.exp(new_probs - old_probs)
引入 entropy 项
def act(self,state):
state = torch.from_numpy(state).float().unsqueeze(0).to(device)
with torch.no_grad():
(mu, sigma) = self.policy(state) # 2d tensors
dist = Normal(mu, sigma)
action = dist.sample()
action_log_prob = dist.log_prob(action)
return action.numpy()[0], action_log_prob.numpy()[0]
(三种策略梯度类算法:Reinforce,PG 和 PPO 我都分别实现了,在 openAI gym 的 cartpole 项目上做了实验,其中 PPO还用了两个版本,相关代码在这里。)
https://github.com/Quantum-Cheese/DeepReinforcementLearning_Pytorch/tree/master/Policy_Gradient
文章最初发表于知乎专栏(作者原创),地址:https://zhuanlan.zhihu.com/p/137120536_