确定性策略梯度算法属于 Actor-Critic 类,综合了 value based 方法和 policy based 方法的优点,在很多任务上的表现能吊打 PG 类算法,比如 gym 的经典难题 BipedalWalker 项目。这里介绍的有两种: DDPG 和它的升级版:TD3,后续还会加入 D4PG 等更多变体的介绍。
算法思想
从 PG 到 DPG,再到 DDPG
PG(Policy Gradient) :随机策略(stochastic policy)通过一个概率分布函数 𝜋𝜃πθ, 来表示每一步的最优策略, 在每一步根据该概率分布进行action采样,获得当前的最佳action取值 𝑎𝑡∼𝜋𝜃(𝑠𝑡|𝜃𝜋)
PG 的缺陷:在高维的action空间的频繁采样,无疑是很耗费计算能力的
DPG( Deterministic Policy Gradient): 即确定性的行为策略,每一步的行为通过函数μ直接获得确定的值 :𝑎𝑡=𝜇(𝑠𝑡|𝜃𝜇)
DDPG是将深度学习神经网络融合进DPG的策略学习方法。
DDPG 也可以看作是 DQN 在连续动作空间的延申
DQN是一种基于值函数的方法,基于值函数的方法难以应对的是大的动作空间,特别是连续动作情况。
传统的 DQN 网络输出各节点对应各离散动作的取值,如果改为对应各动作维度,可以表示连续动作空间(即 DDPG中 critic 网络的输出,)但要在每个维度上用贪婪算法进行最大值搜索是很难实现的,就是要计算每个 state 下对应的所有动作的 Q 值,然后从中找最值。
DQN cannot be straightforwardly applied to continuous domains since it relies on a finding the action that maximizes the action-value function, which in the continuous valued case requires an iterative optimization process at every step.
DDPG 相比于 value based 方法的优势:
DDPG 是基于 Actor-Critic方法,在动作输出方面采用一个网络来拟合策略函数,直接输出动作,可以应对连续动作的输出及大的动作空间。
DDPG 中的 critic 也会输出 Q(s,a)值,但只是 Repaly Buffer 中的部分采样经验对应的值,且无需进行最大值搜索,Q(s,a)只用来训练 actor 策略网络,最终的动作由策略网络直接输出
还有就是 Actor-Critic 类方法本身的优势,可以结合 value based 和 policy based 方法的特点,既能直接给出最佳策略,又能通过 crtic 对候选的 (s,a) 对进行评估,不断修正 actor 的策略
网络架构
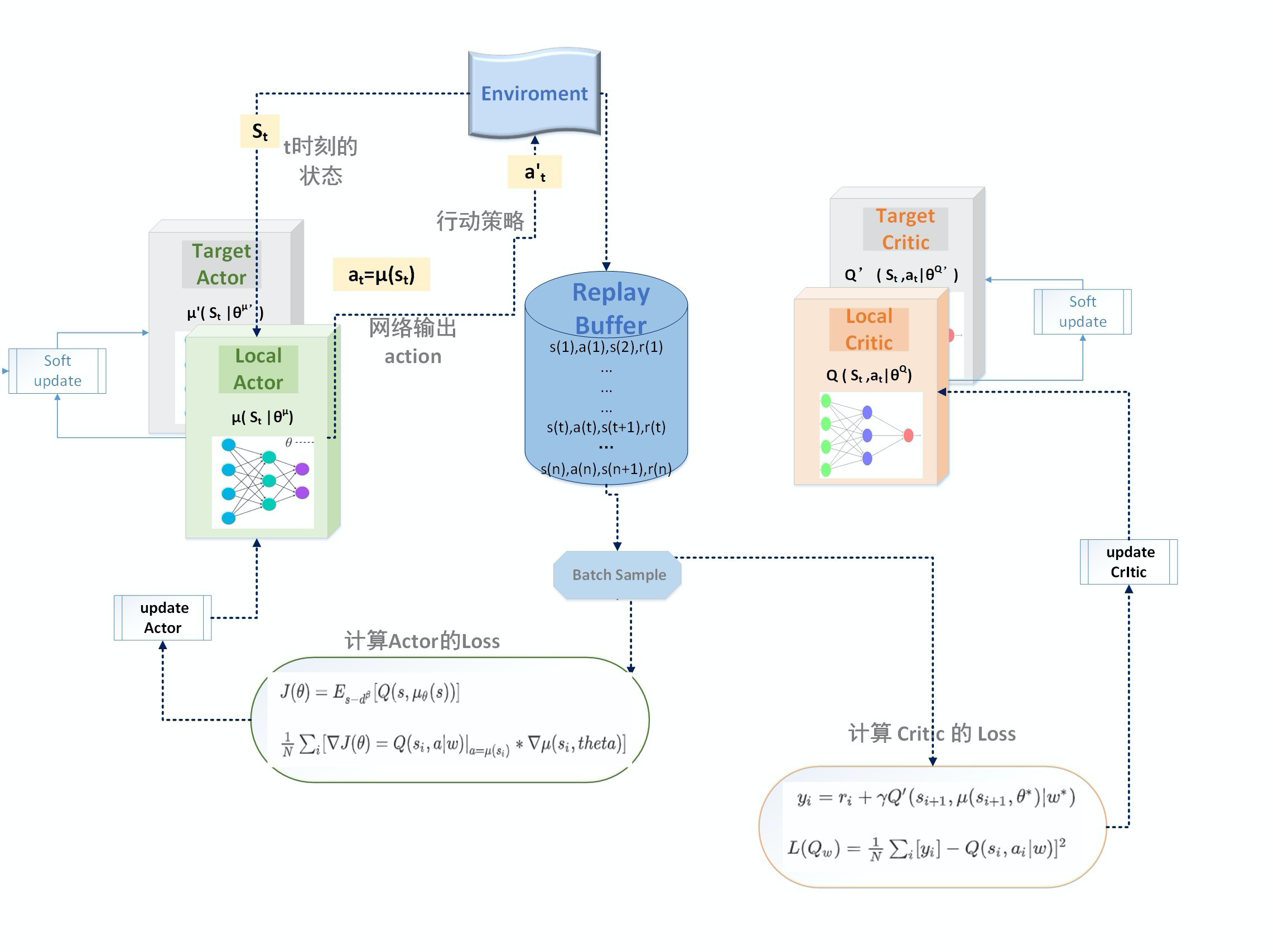
损失函数
Actor 网络的 loss function

Critic 网络的 loss function

算法流程

关键设计
- off policy 随机动作探索

上述这个策略叫做behavior策略,用β来表示, 这时RL的训练方式为离线策略(off-policy)
这里与 ϵ−greedy 的思路是类似的。
DDPG中,使用Uhlenbeck-Ornstein随机过程(下面简称UO过程),作为引入的随机噪声: UO过程在时序上具备很好的相关性,可以使agent很好的探索具备动量属性的环境
这个β不是我们想要得到的最优策略,仅仅在训练过程中,生成下达给环境的action, 从而获得我们想要的数据集,比如状态转换(transitions)、或者agent的行走路径等,然后利用这个数据集去 训练策略μ,以获得最优策略。
在test 和 evaluation时,使用μ,不会再使用β
Soft update (Copy network)
soft update是一种running average的算法 :
\theta ^{Q'} = \tau \theta ^{Q}+ (1-\tau) \theta ^{Q'}
\theta ^{\mu'} = \tau \theta ^{\mu}+ (1-\tau) \theta ^{\mu'}
优点:target网络参数变化小,用于在训练过程中计算online网络的gradient,比较稳定,训练易于收敛。
缺点:参数变化小,学习过程变慢。还有一个问题是使用这种缓慢更新的 target 网络,容易引起对 Q 值的过高估计(over estimation),从而使策略很难收敛,这个缺陷在后续的升级版算法 TD3 中得到了解决。
Repaly Buffer
这里沿用了 DQN 中的经验回放策略,打破经验之间的耦合,每次随机批量采样去训练网络参数。