
今天介绍的Double Q-learning算法,是学习TD3前需要了解的前置工作。论文是DeepMind发表于2015年NIPS上的,作者Hasselt。
原文传送门:https://proceedings.neurips.cc/paper/2010/file/091d584fced301b442654dd8c23b3fc9-Paper.pdf
特色
Q-learning在reward存在随机性时Q value会出现overestimation问题。今天介绍的double Q-learning通过把action selection和value estimation解耦,保留两个Q-function的估计互相更新来减小值估计的偏差。(double Q最后可能得到一个偏低估的Q值估计,后来的TD3在double Q的基础上做了改进使得Q的估计更准确一些)
这篇文章从数学上解释了single estimator为什么会出现Q值高估,提出了double estimator还证明了其收敛性。
回顾Q-learning
The optimal action value function
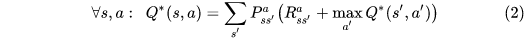
The update of Q-learning
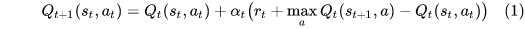
Q-learning还有很多变体比如Delayed Q-learning, Phased Q-learning, Fitted Q-iteration等都是为了加速Q-learning的收敛。Q-learning的收敛速率是experience的指数级,通过选择合适的学习率也可以到达多项式级别。
为什么会出现overestimation?
当reward不是deterministic而是服从某个随机分布时,因为一次采样随机性比较大,可能出现偏离期望的高收益,因为更新Q时有取max Q的操作,这样偏高的reward会被记录下来用来更新迭代,传递下去累加起来就会得到高估的Q值。
这样可能选不到最优的action,于是策略会多访问这样的action,直到经验足够多发现高估,以及通过探索发现了其他更好的action。这很大程度上影响了Q-learning的性能。
(我们目标要估计的是Q function,其定义就是未来reward的期望。后面的文章介绍中我们会讲到distributional RL,根据不同的风险偏好,可以选择估计目标,是未来收益的期望,还是可能的收益上限,还是最低的保底收益等。)
例子
首先通过Sutton书[1]上的例子来直观的看一下:
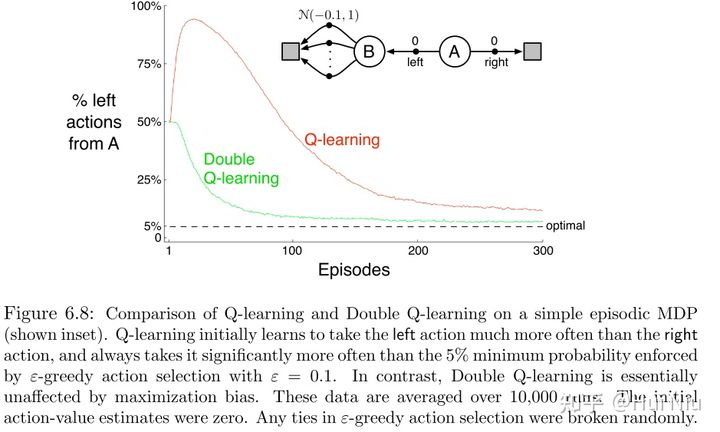
假设从状态A开始,有左右两个action。
往右走会到达终止态并获得0的reward;
而往左边走到达状态B也获得0,而在B状态有10个action都可以到达另一个终点,reward都服从μ为-0.1的正态分布。
可知A状态的最优动作应该是往右。但是Q-learning一开始是偏向向左的,因为B后面reward采样到了正的情况,这样很长一段时间Q左都是>0的。
公式(2)中我们希望对return的期望求max,顺序应该是 [公式] 。但是single-estimator也即Q-learning的做法是采样a时取max,然后多次采样求平均来估计,顺序是 [公式] 。由Jensen's inequality可以得出是高估了Q值。
论文第二节的证明是更加严谨的数学证明。知乎上有很多详细解读,有兴趣的同学可以参考J.Q.Wang的博客: DeepRL系列(6): Double Q-learning算法
我们来简单地看一下主要结论。
估计目标为:

Single-estimator
单估计器的估计方式为
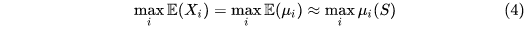

Double Q-learning
根据前面的分析,我们想到了单个估计器中中,具有maxQ估计的action不一定是具有真的最大期望收益的action,这个Q的估计也不准确,二者互相影响变差。如果把action selection和value estimation解耦,用两个Q估计器互相纠偏,可能会消除一下影响。
根据上面的double-estimator,设计了Double Q-learning方法,具体来说就是第一个estimator [公式] 用来选择action,然后用对应的第二个estimator [公式] 的值来更新 [公式] ,而不是自己更新自己。

实验
文章的实验结果也很值得一观。可以看到前面说的低估问题。
实验环境是一个grid world,从起始点S走到终点G,每一步可能收到+10或者-12的随机reward,而到达终点会获得+5的奖励。
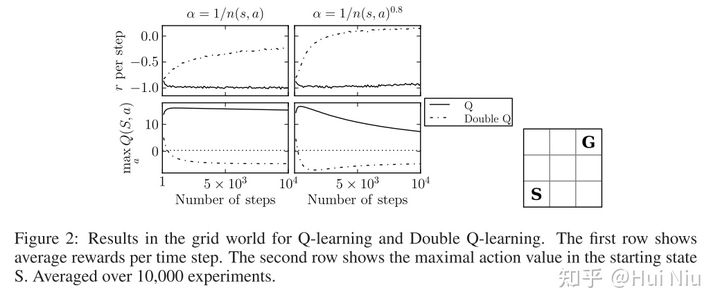
图上第一行显示的是平均每步的reward,第二行是起始点的Q值估计。
由于最优的policy是走5步到达终点,所以最优平均每步reward应该是 [公式] ;起始点的Q值就是1。
从图上看,第一行double Q的表现比Q-learning好很多,说明最后形成的policy还算不错。第二行则说明action选得好不代表对Q的估计就准确,可以发现double Q对Q*是偏低估的。
小结
double Q-learning把选action和估计Q分开来提供了不错的思路,虽然把高估的Q拉下来了,但是又会出现低估问题。而高估低估的本质又和估计方法的期望和max算子的顺序和对象有关系。后面出现的TD3算法将double Q过于低估的Q又回调了一些,取得更准确的估计。