Natural gradient是非常重要的方法,我打算用三篇的篇幅介绍它,分别介绍motivation,计算公式和效果,以及RL上的应用和其他角度的解读。今天这篇主要介绍natural gradient的motivation,它是解决什么问题,以及为什么原有的方法会出现这样的问题。
Natural gradient是Armani在1998年提出并致力于推广的概念。RL中的很多算法都基于natural gradient,比如TRPO和PPO。为了更好地理解基于natural gradient的RL算法,我们先梳理一下natural gradient相关的知识。
Differential geometry和statistical geometry的交叉,是information geometry,natural gradient就是基于information geometry的梯度。它是一种和模型参数化方式无关的梯度,可以解决普通梯度下降方向和参数化方式有关从而效果不好的问题。
现在我们正式开始。Natural gradient是为了解决标准梯度下降方法会受到模型参数化方式影响的问题提出的。
首先我们来回顾一下标准梯度下降。
Standard Gradient Decent
回顾一下标准的梯度下降方法
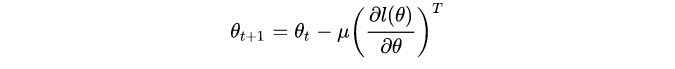
它撒旦是proximal gradient decent的解(proximal gradient decent就是在当前θ附近找一个点对loss进行泰勒展开近似后使得它的loss是周围最小的):
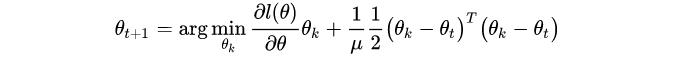
左边的部分是为了找到一个好的方向,而右边的部分也可以理解为不希望找的近似点距离原来的点太远。
那为什么标准梯度下降方法会受到参数化方式影响呢?接下来我们看一下它会有什么问题。
What's Wrong With Standard Gradient Decent?
为了理解开头提到的“梯度方向和参数化方式有关”,我们首先要理解,模型的输出是定义在 [公式] 维流形(manifold)上的概率族(probability family)。而后再分析不同的参数化方式对于流形和概率族会有什么影响。
现在,在supervised learning任务中,我们考虑两个模型为例子:linear regression和Neural Network(NN)。
Probability Family
对于一个概率性的输出模型,我们的数学形式通常是这样的:
输入x 服从input distribution p(x) 。
模型输出也是概率性的p(z: x|\theta) :对分类和回归问题,我们有
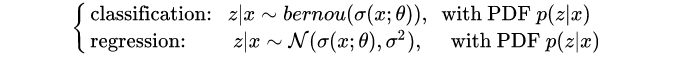
然后我们有一个loss function,比如likelihood和log likelihood函数( t_{i} 是ground truth):
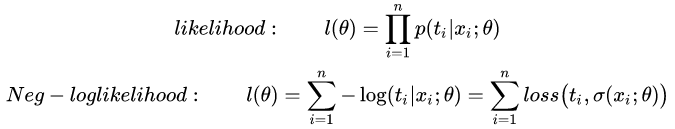
最后,将先验概率和后验概率相乘就可以得到输入和输出的联合分布

论我们以什么方式参数化定义这个线性回归模型,我们都会得到相同的一些probability distributions!(比如都是某些正态分布,只不过参数化方式不太一样。)
尽管我们有很多种参数化方式,但是在线性回归模型中,我们只能有2个互相独立的参数(假设x,z都是一维的)。也就是说,输出的后验概率族定义在一个二维的流形(manifold)上。
事实上,不同的参数化方式会使得流形有不同的基(fundamental),但是流形仍然是同一个。(比如上图画的红线和蓝线代表不同的基,但是它们描述的是同一个流形)
下图有助于理解分布族的流形:
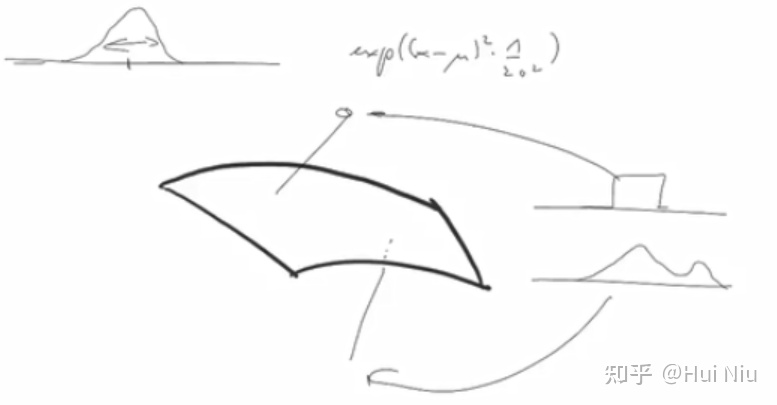
(某个2-D manifold定义了一族正态分布。那么一个其他分布比如方形分布或者双正态分布可能就会在这个流形上方或者下方,总之不在这个正态分布族的流形上,其他分布的流形也不一定是2维的。)

黑色的神经元张成了一个9(6 weights+3 bias)维的流形,多加一个绿色神经元就变成了13 D-manifold
每个神经元的定义方式是任意的,所以NN也有很多参数化方式。
Proximal Operator
讲完了不同的参数化方式对于概率族和流形的影响,接下来我们看一下,proximal operator给出的方向是怎样的。
回顾proximal operator:
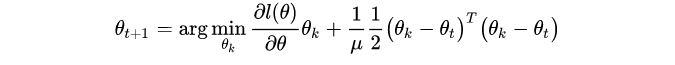
观察右边的正则项,我们发现,对于不同的(任意)参数化方式,proximal operator会给出不同的梯度方向,尽管左边的loss functionl(\theta) 是相同的(是后验的log likelihood)。
例子 为什么会有不同的梯度方向?
观察梯度下降公式
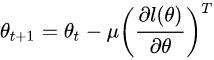
左边参数本身是contravariant的(不同的参数化方式会变),而右边梯度是covariant的。
举2个例子来看:
1)一维例子。当参数化方式从g变为kg时,θ可能需要有1000倍的变化,但梯度不会有。这样在流形图上的方向差别就会很大。
2)二维例子。如下图,有一些限制条件比如正则化\left(\theta_{k}-\theta_{t}\right)^{T}\left(\theta_{k}-\theta_{t}\right),在不同的坐标系(基)下形状是不一样的,给出的方向也不同。
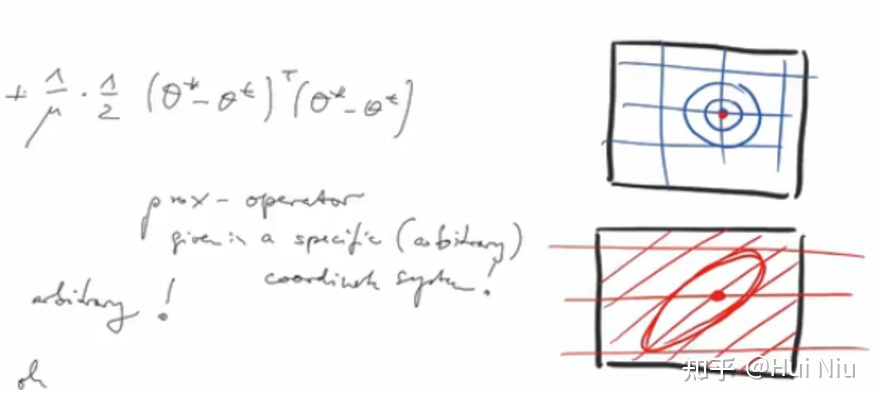
所以,用proximal gradient decent实际上是挑选参数 [公式] 使得loss减小,但使loss减小的方向有很多,具体是哪个方向取决于参数化的方式(the way of parameterization)。
这是不好的。
所以我们希望找到一种和参数化方式无关的,使loss减小最快的方向。这就是natural gradient的motivation了。
接下来的文章,我们会讲natural gradient的计算方式和实验效果。