
强化学习算法TD3 论文:Addressing Function Approximation Error in Actor-Critic Methods 2018.10. ,
作者本人的TD3代码,PyTroch实现: https://github.com/sfujim/TD3
写在前面
与原版DDPG相比,TD3的改动可以概括为:
- 使用与双Q学习(Double DQN)相似的思想:使用两个Critic(估值网络Q(s, a))对动作-值进行评估,训练的时候取min(Qθ1(s,a),Qθ2(s,a)) 作为估计值,这个结构可以用很小的改动加入到其他算法中,在本页面搜索「TwinsCritic的快速应用」即可查看
- 使用延迟学习:更新估值函数的频率大于策略函数
- 使用软更新:更新的时候不直接复制网络参数,而是
- 使用梯度截取:将用于Actor(策略网络)参数更新的梯度截取到某个范围内\theta = \tau\theta^{'}+(1-\tau)\theta
- 使用策略噪声:TD3不仅和其他算法一样,使用epsilon-Greedy 在探索的时候使用了探索噪声,而且还使用了策略噪声,在update参数的时候,用于平滑策略期望。
2019-10-12 初版(开始写的时间)
2019-10-24 发布文章
2019-10-25 增加对封面图的解释:「函数的近似误差是如何导致高估偏差的?」
2019-10-25 自己重新读了一遍,修改了许多错误:TD-learning,延迟更新,发散行为(无法收敛)divergent behavior 等,增加对高估偏差的解读
2020-10-16 不要私信问我其他RL算法的实现了,Github搜索 ElegantRL 就好。
2021-1-14 最优化操作会传播高估误差,低估误差不会被传播
尽管我在翻译的同时已经对信息进行过滤,但是文章依然比较长。阅读正文需要超过20分钟。封面图是TD3算法的核心内容之一,在本页面内搜索「函数的近似误差是如何导致高估偏差的?」可以直接查看。如果文中存在错误争议请指出,我会做出修改。
想要各种深度强化学习算法的实现代码(DDPG、TD3、PPO、SAC),可以看「何须天授?彼可取而代也」用于入门的强化学习库 model-free RL in PyTorch ,或者直接去Github搜索 ElegantRL。
Addressing Function Approximation Error in Actor-Critic Methods 解决AC框架中的函数近似误差问题
Scott Fujimoto - McGill University(加国麦大. 2018.10. arXiv.)
翻译约定」
- 函数近似误差:Function Approximation Error
- AC框架:Actor-Critic** Methods
- 策略函数:Policy** function, Actor、演员
- 估值函数:Value function, Critic、评论家
- 状态 - 值 函数:Q(state, action)、Critic
- Q值高估:overestimated value estimates
- Q值学习:Q-learning
- 深度Q网络:DQN, Deep Q-learning Netwrok
- 双Q学习:Double DQN
- 时间差分学习:TD-learning, Temporal difference learning
- 延迟策略更新:Delayed Policy Updates
- 确定策略梯度:Deterministic Policy Gradient
- 次优的策略 :suboptimal policy
- 次优的动作:suboptimal action
- 时间差分法:TD Method,Temporal Different
0. 摘要 Abstract
众所周知,在基于价值学习的强化学习算法中,如DQN,函数近似误差是导致Q值高估和次优策略的原因。我们表明这个问题依然在AC框架中存在,并提出了新的机制去最小化它对演员(策略函数)和评论家(估值函数)的影响。我们的算法建立在双Q学习的基础上,通过选取两个估值函数中的较小值,从而限制它对Q值的过高估计。我们展示了目标函数与高估偏差之间的联系,并建议使用延迟更新策略以减少每次更新的误差,从而进一步提高了算法性能。我们在OpenAI上的一整套任务上估值了我们的方法,并且在每个任务环境中都展现出了最高水平(2018.10.)。
1. 介绍 Introduction
在离散动作的强化学习中,对「Q值高估的问题由函数近似误差造成」已经有了很好的研究。然而,在连续动作控制的AC框架中,相似的问题还没有被触及。在本文中,我们表明了 造成 对Q值的过高估计以及对误差的累积 的结构存在于AC框架中。我们提出的方法解决了这些问题,并且算法性能展现出了最高水平(2018.10)。
Q值高估 OverEstimation Bias 是Q值学习的一个特性。对含有噪声的的Q值进行最大化时,估值函数会持续地高估Q值。当估值函数学习对真实值进行逼近时,噪声将不可避免地降低估值函数的准确度。由于这些方法依据贝尔曼方程,使用后续状态对估值函数进行更新。TD-learning(时间差分学习 Temporal Difference learning)的这种性质加剧了精确性的下降。这意味着在每一次更新策略时,使用一个不准确的估计值将会导致错误被累加。这些被累加的错误会导致某一个不好的状态被高估,最终导致策略无法被优化到最优,并使算法无法收敛(divergent behavior)。
本文建立在Q值高估 OverEstimation Bias 是Q值学习的一个特性的基础上,所有基于Q值学习的强化学习算法都存在着这个问题。 对连续动作进行控制的确定性策略梯度算法DPG 也存在Q值高估的问题。此外,我们发现 的离散动作进行控制的双Q学习中普遍存在的解决方案在 AC框架中无效。训练期间,双Q学习通过一个离散的目标价值函数对当前策略的价值进行估值,允许在没有最大化偏差(maximization bias)的时候对动作进行估值。不幸的是,由于在策略更新缓慢的AC框架背景下,当前价值与目标价值的估值依然过于相似 而无法避免最大化偏差。... ...(提到了以往的解决方案)... ...
考虑到估值函数中的噪声与Q值高估偏差的关系,我们提出了一些解决方法:
- 为了解决估值函数与策略函数的耦合问题,我们建议延迟更新策略函数,直到价值函数收敛为止。
- 使用目标网络是Q值学习中的一种常见的方法,它对于通过减少错误的累积从而减少方差(variance reduction)
- 我们采用了与SARSA相似的方法用以进一步减少方差。就是在计算Q值的时候,给动作加上比较小的噪声,使用这样子计算出来的动作估值对估值网络进行训练
译者注:方差 variance,在文中不断出现,我认为它指的是:估值网络的估值与真实值之间的误差的方差。如 Section 5 解决方差问题 Addressing Variance,意思是:解决由于估值函数对真实值拟合不精确 带来的方差问题。
我们将这些修改应用到DDPG(深度确定性策略梯度)算法上,然后把它称为TD3算法(双延迟深度确定性策略梯度 TDDD Twin Delayed Deep Deterministic Policy Gradient),它是一个考虑了 AC框架中策略函数与估值函数中间的函数近似误差之间相互影响的 算法。这个算法开源在Github上: TD3代码的PyTroch实现。
2. 相关工作 Related Work
函数近似误差以及它对偏差和方差的影响已被前人研究了。由估值函数存在近似误差从而导致了强化学习智能体训练中的两个问题 是我们研究的重点,即 Q值高估偏差(OverEstimate bias) 和 高方差累积(High Variance Build-up)。
在Q值学习中,存在一些降低 由于函数近似和策略优化导致的 Q值高估偏差 的方法。双Q学习使用两个独立的估值函数来得到对动作的无偏估值。其他方法注重于直接降低方差,最小化早期对高方差估计的过拟合,或者通过修正项达到这个目的。... ...(提到了以往的解决方案)... ...
3. 背景 Background
译者注:背景部分讲的是强化学习概述,可能是写给不懂强化学习的审稿人看的,建议跳过
强化学习考虑了 代理智能体(agent)与其环境交互的范式(paradigm),其目的是使智能体采取最大化收益的行为。
- 把连续的时间分为离散的多个时刻t
- 每个状态s 都存在于集合S中
- 每个动作a 都存在于集合A中
- 智能体通过π策略,对状态s 做出对应的动作a
每个时刻,采用π 策略的智能体会根据状态s 选择对应的动作a ,然后与环境交互,得到这一步的收益r,以及下一步的状态s'。回报被定义为收益的折扣总和(discounted sum):
R_{t}=\sum_{i=t}^{T} \gamma^{i-t} r\left(s_{i}, a_{i}\right) 里面的\gamma \in(0,1) 是一个用于确定短期奖励优先级的折扣因子。
在强化学习中,智能体的目标是寻找一种 \phi 参数下的最优策略\pi_{\phi},它可以最大化收益函数:J(\phi)=\mathbb{E}_{s_{i} \sim p_{\pi}, a_{i} \sim \pi}\left(R_{0}\right)(收益函数对策略进行估值,计算了采用此策略后的状态转移与动作选择的智能体所获得的收益期望R0)。通过对动作的连续控制,参数化的策略 \pi_{\phi}可以用估值函数提供的梯度 \nabla_{\phi} J(\phi) 。在AC框架中,策略函数(也被称为Actor)通过确定性的策略梯度算法进行策略更新:
\nabla_{\phi} J(\phi)=\mathbb{E}_{s \sim p_{\pi}}\left[\left.\nabla_{a} Q^{\pi}(s, a)\right|_{a=\pi(s)} \nabla_{\phi} \pi_{\phi}(s)\right]
其中,Q^{\pi}(s, a)=\mathbb{E}_{s \sim p_{\pi}, a \sim \pi}\left[R_{t} \mid s, a\right],其中期望收益是在状态s 是,遵从π策略,做出动作a 得到的预期收益,这个收益通过估值函数Q^{\pi}(s, a)(critic)得到。
在Q值学习算法中,估值函数可以使用基于 贝尔曼方程(Bellman equation 连续收益方程) 延迟学习(TD-learning Temporal difference learning)。连续收益方程描绘了 当前时刻 与的一对【状态,动作】(s, a) 的收益 与 下一时刻的一对【状态,动作】(s', a') 的收益 之间的关系:
Q^{\pi}(s, a)=r+\gamma \mathbb{E}_{s^{\prime}, a^{\prime}}\left[Q^{\pi}\left(s^{\prime}, a^{\prime}\right)\right], a^{\prime} \sim \pi\left(s^{\prime}\right)
评估函数Q( · )根据 一对状态与动作,对策略π 进行评估。它等于 当前这一时刻的收益 加上乘以折扣率的下一步的期望收益。期望收益E 是根据π策略采取行动得到的 下一时刻的 一对状态与动作计算出来的。因此计算期望收益时,下一时刻的动作a' 也是根据π 策略在下一时刻的状态s' 下得到的。
贝尔曼方程(Bellman方程,连续收益方程)也可以这样子解释:针对一个MRP过程(连续状态奖励过程),状态S转移到下一个状态S' 的概率的固定的,与前面的几轮状态无关。其中,v( · )表示一个对当前状态state 进行估值的函数。可以看到等式的右边也有 v( · ),连续状态估值方程可以迭代地计算了收益值。 [公式] 是折扣因子,取一个01的数字,接近1且小于1。v(s)=\mathcal{R}_{s}+\gamma \sum_{s^{\prime} \in \mathcal{S}} \mathcal{P}_{s s^{\prime}} v\left(s^{\prime}\right)
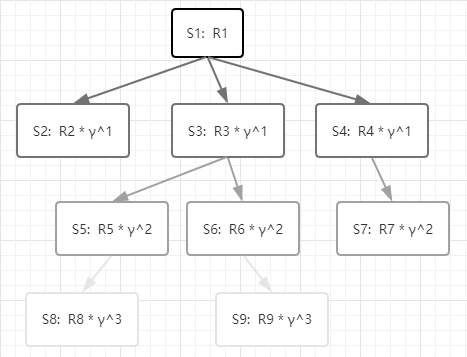
这幅图是译者画的「贝尔曼方程如何计算连续动作的收益?」,每个状态S都对应了收益R,折扣因子 γ: gamma 的指数是距离当前状态的步数。因此处于越远未来的收益对当前这一步收益的影响越小(在图中颜色越淡)。
对于一个巨大的状态空间,评估值可以通过一个参数为θ 的可微分近似函数Q^{\pi}(s, a)(估值函数)得到。在深度Q值学习算法中,网络通过使用延迟学习的方法,在训练策略函数双时候,冻结了用于辅助其参数更新的估值网络,使用估值网络传出的梯度用于更新策略网络自己的参数,在多次的更新中保持固定的目标y:
y=r+\gamma Q_{\theta^{\prime}}\left(s^{\prime}, a^{\prime}\right), a^{\prime} \sim \pi_{\phi^{\prime}}\left(s^{\prime}\right)
译者:请注意,估值函数 Q( · ) 的参数是 θ,而策略函数 π( · )的参数是 。
译者:请注意,无论这个函数是估值函数还是策略函数,如果它是用于参数更新的「当前函数 Current Network」,那么它会在右上角加上一点 ’,如 \theta^{\prime}, \phi^{\prime} 。如果它是延迟学习中,我们最后要输出为训练结果的函数,那么它没有加点,如\theta^{\prime}, \phi^{\prime} 。
译者:请注意,由于TD3算法里面有一个策略函数(actor),和两个估值函数(critic),一共3个,再加上使用了延迟更新,所以3×2 == 6,请没有自己复现过TD3 算法的读者注意区分。
目标网络(目标函数)的权重被周期性地更新,比如每过N步,算法将当前函数的参数更新到目标网络上。同时可以使用软更新,软更新公式为:\theta = \tau\theta^{'}+(1-\tau)\theta ,软更新可以应用到使用记忆回放的那些异策略的方法上。
译者注:异策略 off-pilicy 与 同策略 on-policy。
强化学习中on-policy 与off-policy有什么区别? ,多看几个答案。
TD3基于DDPG,DDPG基于DQN,DQN基于Q-learning,而Q-learning就是异策略,里面的策略函数没有直接在环境中学习,而是隔着一个估值网络与间接地与环境进行交流:策略网络做出一个动作后,根据估值网络的评价对动作进行评估。
而PPO(近端策略优化)基于TRPO,TRPO(信任域策略优化)基于SARSA,SARSA就是同策略,它直接与环境进行交流:策略网络做出一个动作后,直接在环境中进行尝试,然后直接对自己进行优化。(进行动作选择的神经网络函数,与 根据Q值进行参数更新的神经网络 是同一个)
本质区别在于:更新Q值时所使用的方法是沿用既定的策略(on-policy)还是使用新策略(off-policy)(用户名为「已注销」的回答)
4. Q值高估偏差 OverEstimation Bias
在离散动作的Q值学习算法中,策略网络通过最大化贪婪目标y 完成参数的更新: y=r=\gamma \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime}\right) 。然而,如果目标y 容易受误差\epsilon影响,那么这个有误差的动作价值估计的最大值通常会比真实值更大。\mathbb{E}_{\epsilon}\left[\max _{a^{\prime}}\left(Q\left(s^{\prime}, a^{\prime}\right)+\epsilon\right)\right] \geq \max _{a^{\prime}} Q\left(s^{\prime}, a^{\prime}\right) 。结果造成:即便最初的误差其均值为0,也会导致价值更新导向一致的高估偏差,然后这个误差会通过贝尔曼方程传播(连续收益方程)。这是一个很大的问题,是由函数近似估计引发的这些误差是不可避免的。
尽管在离散动作的背景下,高估偏差是通过解析最大化(analytical maximization)人为引入的一个明显痕迹(obvious artifact)。但在使用梯度下降进行更新的AC框架背景下,高偏估计的出现原因与其影响还不太清晰。在一开始的4.1 节中,我们先证明确定策略梯度在满足一些基本假设的背景下会存在高估偏差,然后在4.2 节中,我们提出了AC框架下的对双Q值学习的梯度方差进行裁剪用以降低高估偏差。(本章节不对对公式中于字母符号的解释进行翻译)
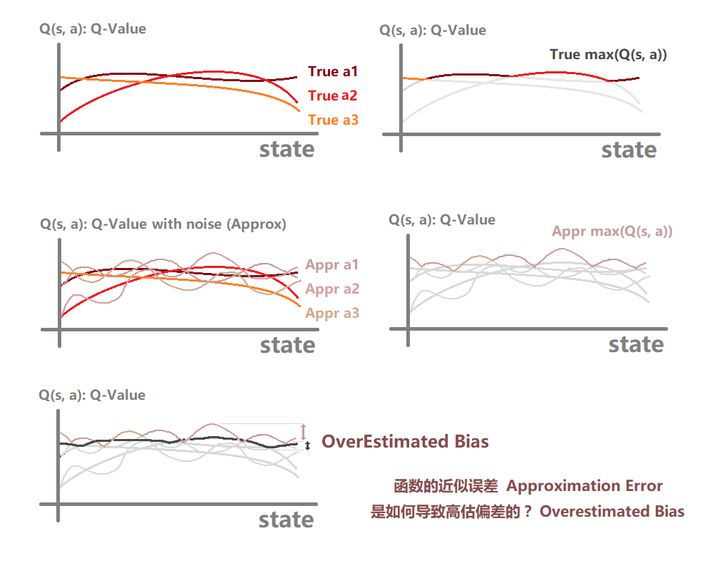
译者注:下面的一段文字与图片是译者自己提供的,我认为原文没有说清楚,既然这样,就由我来帮原文解释「 函数的近似误差是如何导致高估偏差的?」吧
4.0.「函数的近似误差是如何导致高估偏差的?」见下图
第一行,不同的动作a1,a2,a3在不同状态下的动作真实值。右边是对估值函数进行解析最大化操作 \max (Q(s, a)) ,不同action下最顶部的曲线被选中。
第二行,不同的动作a1,a2,a3在不同状态下的动作估计值,由于是估计值,所以带有噪声,与真实值的曲线不完全重合,只是围绕在真实曲线的周围,噪声越大,拟合曲线与真实曲线的偏离就越大。右边也做了解析最大化的操作。可以看到,由于噪声的存在,虽然某个动作被高估和低估的可能性相同,但是经过最大化操作后,被高估的那段曲线更容易被选中。噪声越大,被高估的可能性、被高估的程度越大。这非常不好。
第三行,由于近似误差导致的高估偏差开始现象。可以看到,当我们把两条解析最大化曲线画到一起时,可以看到在绝大部分区域,被噪声影响的最大化曲线 都是大于真实值的,且随着参与评估的动作增大,被高估的可能性也会增大。在DQN这一类动作空间离散的算法中,这个现象会存在,那么在DDPG这一列动作空间连续的算法中,这个现象只会更加普遍。
注意,单次估值计算只是被高估的可能性大,而不是一定会被高估。存在高估偏差还因为:“被高估的值,容易通过多次更新得到传播与累积”。因此多次更新后,高估偏差才会越来越大。
4.1. AC框架中的高估偏差 Overestimation Bias in Actor-Critic
在强化学习AC框架中,策略函数的参数更新与估值函数对动作价值的估计有关。在这一节里面,我们假设策略函数使用确定策略梯度进行参数更新,并表明由这种更新会导致的动作价值被高估。
\begin{aligned}
\phi_{\text {approx }} &=\phi+\frac{\alpha}{Z_{1}} \mathbb{E}_{s \sim p_{\pi}}\left[\left.\nabla_{\phi} \pi_{\phi}(s) \nabla_{a} Q_{\theta}(s, a)\right|_{a=\pi_{\phi}(s)}\right] \\
\phi_{\text {true }} &=\phi+\frac{\alpha}{Z_{2}} \mathbb{E}_{s \sim p_{\pi}}\left[\left.\nabla_{\phi} \pi_{\phi}(s) \nabla_{a} Q^{\pi}(s, a)\right|_{a=\pi_{\phi}(s)}\right]
\end{aligned}
其中,Z1与Z2用于对梯度进行归一化,有Z^{-1}\|\mathbb{E}[\cdot]\|=1。如果没有对梯度进行归一化,那么在稍微严格的条件下高偏估计仍然保证会发生。我们在补充材料中还将进一步考究这个问题。(我没有忠诚地翻译4.1章的内容,因为下文标记为灰色字体,有需要请看原文)
译者注: \phi_{\text {approx }} 表示根据近似估值更新得到的策略函数 \pi的参数,\phi_{\text {true }} 表示根据(理想中的)真实估值更新得到。强化学习的目的就是希望训练得到的策略函数的参数尽可能接近真实值\phi_{\text {approx }} \rightarrow \phi_{\text {true }} 。
由于使用梯度方向进行更新就是一种求局部最大化的操作(the gradient direction is a local maximizer),因此存在一个足够小的数 [公式] 与足够大的数[公式]使得对应的 approx1 与 approx2 的期望比实际值更小或者更大:
\mathbb{E}\left[Q_{\theta}\left(s, \pi_{\text {approx1 }}(s)\right)\right] \geq \mathbb{E}\left[Q_{\theta}\left(s, \pi_{\text {true }}(s)\right)\right] \geq \mathbb{E}\left[Q_{\theta}\left(s, \pi_{\text {approx2 }}(s)\right)\right]
尽管每一次更新被高估的可能性小,但是这个错误引发了两个问题:一、如果不对高估进行检查,那么在多次更新后,这个高估偏差会越来越明显。二、一个不准确的估计值会导致训练出不好的策略。 这是相当严重的问题,这引发了一个不良的反馈循环。次优的估值网络可能会高度评价一个次优的动作,并在下一次的梯度更新中强化(reinforcing)这个次优的动作。
译者:可能「强化学习」(reinforcement learning 增强学习)之所以这么命名,是因为各种算法的reward系统 可以让某个正确的选择在下一次梯度更新后得到「强化」
这个理论上的会出现的Q值高估现象在 当前最高水准的算法里面也会出现吗?(原文加粗)答案:「会」。TD3 2018.10,DDPG 2015,OpenAI的环境 Hopper-v1 与 Walker2d-v1 2016。
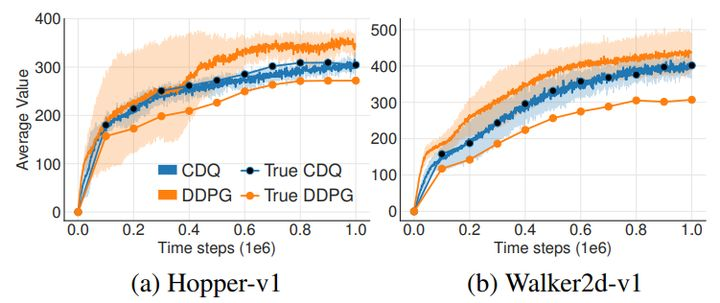
CDQ(Clipped Double Q-learning)进行梯度截取的Q值学习,DDPG(深度确定策略梯度),可以看到使用了梯度截取的放它的平均估值要更低。这个数据是在OpenAI-Gym-MuJoCo(三维环境中的机器人动作任务)中完成的。
译者注:我在LunarLanderContinuious-v2 和 BipedalWalker-v2 上面尝试,启用TD3 里面的 Twins Critic结构的确可以让Q值变得更小。如果训练期间发现Q值持续增大,然而实际上智能体在环境中并没有持续变好,那么这个时候使用TD3 的 min(q1, q2) 就很恰当。
4.2. 在强化学习的AC框架中 截取双Q值学习的梯度 Clipped Double Q-Learning for Actor-Critic
现今已经有一些降低高估偏差的方法被提出来,但是我们发现在AC框架中它们不起作用。这一节包括了双Q值学习的一种新的梯度方差截取方法,这种方法可以取代任何AC框架中估值网络原有的方法。
在双Q值学习中,通过维持两个单独的估值函数,可以将贪婪更新从估值函数中剥离(disentagled)出来。如果估值是独立的,那么通过使用另一个估值网络的估值(opposite value estimate)来选择动作,这使得这些独立的估值可以被用做无偏估计。在双Q值学习中,其作者使用目标网络作为其中的一个价值估计,并通过贪婪算法选择估值最大的动作来最大化当前的估值网络 而非目标网络。在AC框架中,相似的更新方法使用当前策略网络而不是目标策略网络: y=r+\gamma Q{\theta^{\prime}}\left(s^{\prime}, \pi{\phi}\left(s^{\prime}\right)\right)(译者注:式子中的theta 是带点的,用于表示 目标网络target network的参数,不带点的表示当前网络 current network。)
当前的估值网络 与 目标网络,指代的是:使用延迟学习时,使用梯度更新当前网络,然后定期把参数更新(直接复制 或者 软更新)到目标网络。
然而,在AC框架中实际操作的时候,我们发现这样做使得策略函数的改变缓慢,当前网络与目标网络过于相似,以至于无法进行独立估计 并且对策略几乎没有提升。反而这种方法可以在原版的双Q值学习中使用:两对不同参数 且有不同的优化目标的Actor-Critic:
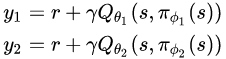
我们对比了原始的Q值学习与双Q学习,可以从下图看到:平均估值曲线总是在 真值曲线的上方,也就是说存在「高估偏差」。尽管双Q学习的高估偏差更小,其算法更有效,但是它也没有完全消除高估现象。
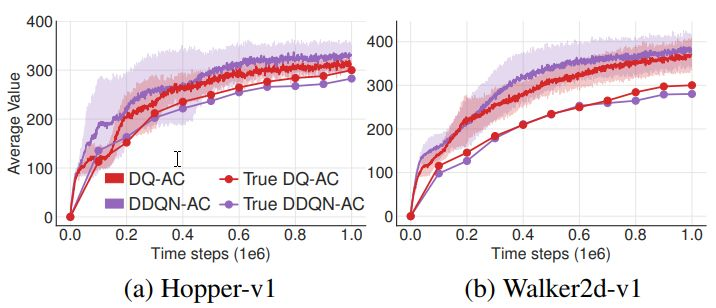
对比了两种双Q学习算法,一种是原始的Q值学习,红色:DoubleQ(DQ);另一种是深度Q值学习,紫色:Double DQN(DDQN)。下方的折线表示真实的Q值,上方带有方差的是学习曲线。在OpenAI 的三维机器人动作训练环境MuJoCo中 训练了十万步(1e6)得出来的结果。
由于策略函数的更新与一个独立估计的估值函数有关,因此可以避免策略更新时引入的偏差。然而估值函数并非完全独立,由于使用了学习目标中的另一个估值函数(the opposite critic in the learning targets) 以及 相同的记忆回放缓存,估值函数并非完全独立。这是有问题的,因为估值函数通常会高估,并且在状态空间的某些区域中,高估现象会被进一步放大。为了解决这些方法我们提出:... ...(由译者来解释的话,是:估值网络在\max (Q(s, \pi(s))的影响下,其估值都偏高,既然如此,我用两个估值网络Q1 与Q2 使用相同的记忆同时进行估值,那么用\min \left(Q_{\theta_{1}}(s, a), Q_{\theta_{2}}(s, a)\right)选出那个高估地更少的作为估计值,可以缓解高估现象,注意这里是缓解而非消除), 用公式表达是:
y_{1}=r+\gamma \min _{i=1,2}\left(Q_{\theta_{i}}\left(s^{\prime}, \pi_{\phi_{1}}\left(s^{\prime}\right)\right)\right)
与标准Q值学习相比,使用了双Q值学习并截取梯度的算法 其价值目标不会被高估。尽管使用这种更新规则会导致低估偏差(underestimation bias),但是低估比高估要好得多,因为动作被低估后,被低估误差不会通过策略更新被传播。
... ... 我们在补充材料中提供「对双Q值学习的梯度进行截取 其算法也能收敛」的证明... ... 动作价值被低估有利于训练的稳定进行... ...
5. 解决方差问题 Addressing Variance
第4章处理了方差对高估偏差的影响,我们还认为需要直接解决方差自己的问题。除了对估值的影响,高方差估计为策略更新带来了有噪声的梯度。这会降低学习速度并影响实际性能(训练质量)。在这一章中,我们强调了在每一次训练中最小化误差的重要性,建立了目标网络与估计误差的联系,并提出了一个学习流程(learning procedure)的用于AC框架减少方差的变体。
5.1. 累积误差 Accumulating Error
由于时间差分更新(TD,Temporal Different Update),使用了 后续状态的估值 对当前状态进行估值,因此会产生误差。尽管在预期中单个更新的误差很小,但是这些估计误差会(在贝尔曼方程/连续价值方程中)得到累积,从而导致较大的高估偏差以及更新出次优的策略。在估值函数对真值的近似存在误差的情况下,这个错误将在不完全满足使用条件的贝尔曼方程中被恶化,并且每一次更新都会残留有一些TD-error\delta(s, a)
Q_{\theta}(s, a)=r+\gamma \mathbb{E}\left[Q_{\theta}\left(s^{\prime}, a^{\prime}\right)\right]-\delta(s, a) :
可以证明,价值估计拟合并不是我们期望的“预期收益的估计”,而是“预期收益的估计”减去“未来TD-error”的期望:
\begin{aligned}
Q_{\theta}\left(s_{t}, a_{t}\right) &=r_{t}+\gamma \mathbb{E}\left[Q_{\theta}\left(s_{t+1}, a_{t+1}\right)\right]-\delta_{t} \\
&=r_{t}+\gamma \mathbb{E}\left[r_{t+1}+\gamma \mathbb{E}\left[Q_{\theta}\left(s_{t+2}, a_{t+2}\right)-\delta_{t+1}\right]\right]-\delta_{t} \\
&=\mathbb{E}_{s_{i} \sim p_{\pi}, a_{i} \sim \pi}\left[\sum_{i=t}^{T} \gamma^{i-t}\left(r_{i}-\delta_{i}\right)\right]
\end{aligned}
如果对动作价值估计的是 未来奖励与估计误差的和,那么估计的方差 将与这个估计值成正比。如果选择更大的γ(折扣因子gamma),倘若我们还没有驯服它(if the error from each update is not ramed),那么方差将会在每一次更新中迅速地增长。此外,每一次梯度更新只是相对于小批次的更新来说 其误差有所减少,而小批次更新的误差大小是没有保证的(译者注:因此这样子做不能保证得到更小的误差)。
5.2. 目标网络与延迟更新 Target Networks and Delayed Policy Updates
译者注:这一节原文过于详细,可能是写给不懂强化学习的审稿人看,因此我做了简要翻译,并写在括号里。
周所周知,目标网络在深度强化学习中被用于稳定网络训练。深度神经网络需要多次梯度更新才能收敛并拟合目标,而使用目标网络可以更新提供一个稳定的目标,从而允许网络拟合更大范围的训练数据。
为了更加直观地理解,我们比较了不同tau值对策略学习的影响,蓝色tau=1表示使用硬更新,tau=0.01是TD3代码中使用的默认值。下图左(a)表示使用固定的策略网络进行学习,并且这个策略网络的动作平均价值红色水平线(固定了当然是一个定值)。可以看到tau值越接近于1,网络的“预热”时间越短。下图右(b)没有把策略函数固定住,而是让策略函数跟着估值函数一起学习,可以看到:在一开始的地方,策略网络被估值网络带歪了,动作平均价值大幅下降,然后发生波动,tau值越接近于0.01时,其波动小(证明使用目标网络的确可以稳定训练),但是训练速度也慢了下来。
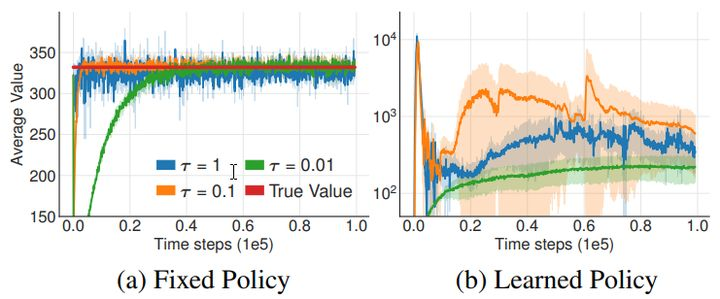
什么情况下,AC框架的学习是失败的?可能因为Actor 和 Critic 之间的相互作用引发了失败。当估值函数不准确的时候,策略函数会根据不准确的估值朝错误的方向进行更新,更新后的记忆用于训练估值函数,估值函数与真实情况出现差异,最终导致估值函数与策略函数的劣化循环。(和对抗网络很像)
... ... 策略网络的更新频率应该低于估值网络,以保证在策略更新前先将估计误差降低。我们提出:应该先把价值误差降低后才进行延迟策略更新。确保 TD-error 足够地小。在降低更新频率的同时,还应该使用软更新:\theta^{\prime} \leftarrow \tau \theta+(1-\tau) \theta^{\prime}
5.3. 目标策略的平滑正则化 Target Policy Smoothing Regularization
确定策略梯度算法中一个担忧的问题是:估值函数的过拟合现象。为此,我们模仿SARSA(相似的行为应该具有相似的价值 similar acions should have similar value),引入一种正则化策略用于平滑目标策略。虽然神经网络的函数逼近会隐式地(implicitly)体现这种操作,但是我们仍然可以对训练流程进行修改,用以显式地体现这种联系:
y=r+\mathbb{E}_{\epsilon}\left[Q_{\theta^{\prime}}\left(s^{\prime}, \pi_{\phi^{\prime}}\left(s^{\prime}\right)+\epsilon\right)\right]
该公式通过自举(bootstrapping)的方法对动作值进行估计,有使估值平滑的优点。实际使用的时候,我们可以添加一个小方差的噪声到目标策略,并平均小批次更新动作期望值:
\begin{aligned}
&y=r+\gamma Q_{\theta^{\prime}}\left(s^{\prime}, \pi_{\phi^{\prime}}\left(s^{\prime}\right)+\epsilon\right) \\
&\epsilon \sim \operatorname{clip}(\mathcal{N}(0, \sigma),-c, c)
\end{aligned}
凭直觉地说:周所周知,直接从SARSA值进行估算会更加地安全,因为他们为抗干扰的行为提供了较高的估值(provide higher value to actions resistant to perturbations)。(译者非常认同此观点,仅限于机器人连续动作训练任务)。
TD3:Twin Delayed DDPG算法

6. 实验 Experiment
6.1. 评估 Evaluation
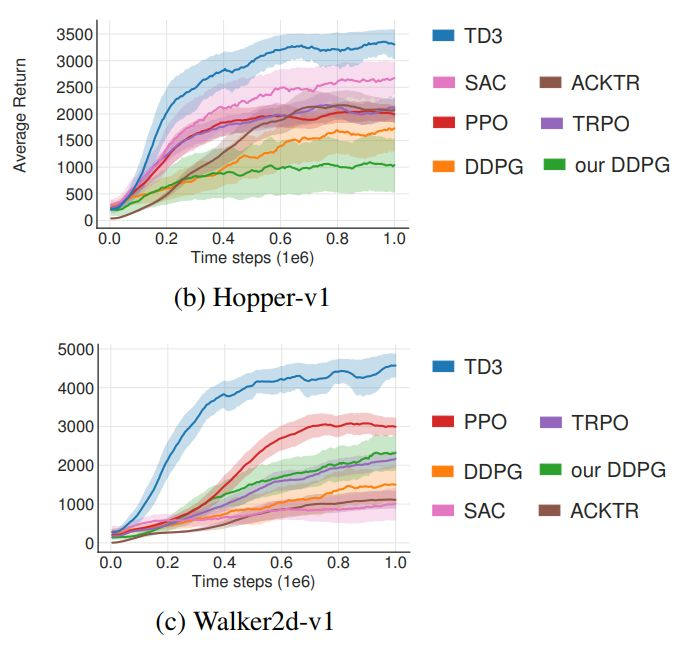
译者注:上图截取了论文提供的部分结果,这份比较结果大家看看就好了。应该多训练几步看每种算法能达到的最高分数,而不是向上面一样只比较了前1e6步的结果,这样子只能显示得出TD3训练地快。在这种比较下,似乎显得其他算法很差,其实展示出多训练几步的结果,才能让TD3宣称自己在2018.10 取得state of the art 更有底气。
按照我自己实际复现的结果看:在2019年上旬,现世的强化学习算法中,兼顾训练速度与训练质量的:TD3、SAC (DDPG的变体)PPO(非AC框架的算法)
欢迎持有与我不同观点的人在评论区推荐其他好用的算法,请给出开源的代码以及其对应的任务环境,没有开源的算法一律当不存在处理。
6.2. 消融实验(模型简化实验) Ablation Studies
被简化掉的结构有:
- 延迟策略更新 DP,Delayed Policy updates
- 目标策略平滑 TPS,Target Policy Smoothing
- 双Q值学习梯度截取 CDQ,Clipped Double Q-learning(译者注:这个结构去掉后对算法的影响稍微大一点,其他消融结果差别挺小的,要么就是没有什么规律)
- TD3的整个架构,超参数以及探索结构 AHE,Architecture, Hyper-parameters, Exploration
7. Conclusion
在基于价值估计的方法中,动作价值高估是一个关键问题。本文中,我们推导了高估偏差也存在于强化学习的AC框架中,...(译者注:这两段话前面写过了,就是第1、4、5章的内容)...
与DDPG相比,基于DDPG修改出来的 Twin Delayed Deep Deterministic policy gradient (TD3,TDDD) 算法既提升了训练效果,也缩短了训练时间,并且算法易于在其他AC框架中实现。译者注:的确易于实现,如下 ↓「TwinsCritic的快速应用」。
「TwinsCritic的快速应用」
作者在Github 上的代码在文章发表出来后更新过,新写法可以用很小的改动将双Q学习应用到其他强化学习AC框架的算法(一般是策略梯度算法)中去:
import torch
...
class Critic(nn.Moudule):
def __init__(self):
super(Critic, self).__init__()
self.network_1 = XXX
self.network_2 = XXX # 新增一个与 netwrok_1 结构完全相同的网络
def forward(self, state, action): # 注意此处,直接把两个网络写在一起,这样就可以只用一个梯度下降优化器
tensor0 = torch.cat((state, action), dim=1)
tensor1 = self.network_1(tensor0)
tensor2 = self.network_2(tensor0)
return tensor1, tensor2
def q1(self, state, action): # 新增一个Q值输出的方法,只使用其中一个网络的结果作为输出,避免重复计算
tensor0 = torch.cat((state, action), dim=1)
tensor1 = self.network_1(tensor0)
return tensor1
...
# 在使用贝尔曼方程(连续状态奖励方程)计算估计值的时候
q_target1, q_target2 = cri_target(next_state, next_action)
q_target = torch.min(q_target1, q_target2) # q_target_next
q_target = reward + done * self.gamma * q_target
...
# 在计算Critic的loss时
q_eval1, q_eval2 = cri(state, action)
cri_loss = (criterion(q_eval1, q_target) + criterion(q_eval2, q_target)) * 0.5
# criterion↑ 是损失函数,如MSE, L1, etc.
...
# 在计算Actor的loss时
act_loss = cri.q1(state, act(state))