今天我们继续讲优化问题中的自然梯度（nature gradient in optimization）。

上篇我们讲到，模型的输出是一个概率族，定义在某个流形（manifold）上，而不同的模型参数化方式会对应不同的基（或者坐标系）。标准的梯度下降法给出的方向依赖于参数化方式。

因此，我们的目的是找到一个和参数化方式无关的梯度下降方法（Parameterization-independant Decent Direction），这就是natural gradient decent。

上一篇文章： http://deeprlhub.com/d/488-typical-rl-03natural-gradient1

Natural gradient decent的思想就是用模型output distribution的变化来衡量参数更新前后带来的变化（约束参数不要走太"远"），而不是像proximal gradient decent中直接使用、theta的变化来构成右边的正则项。

那怎样衡量输出分布的变化呢？今天我们会讲，KL-divergence是一个很好的方式，并且可以推出neuron manifold上的黎曼度量张量（Riemannian metric tensor）是Fisher Information Matrix（FIM）。

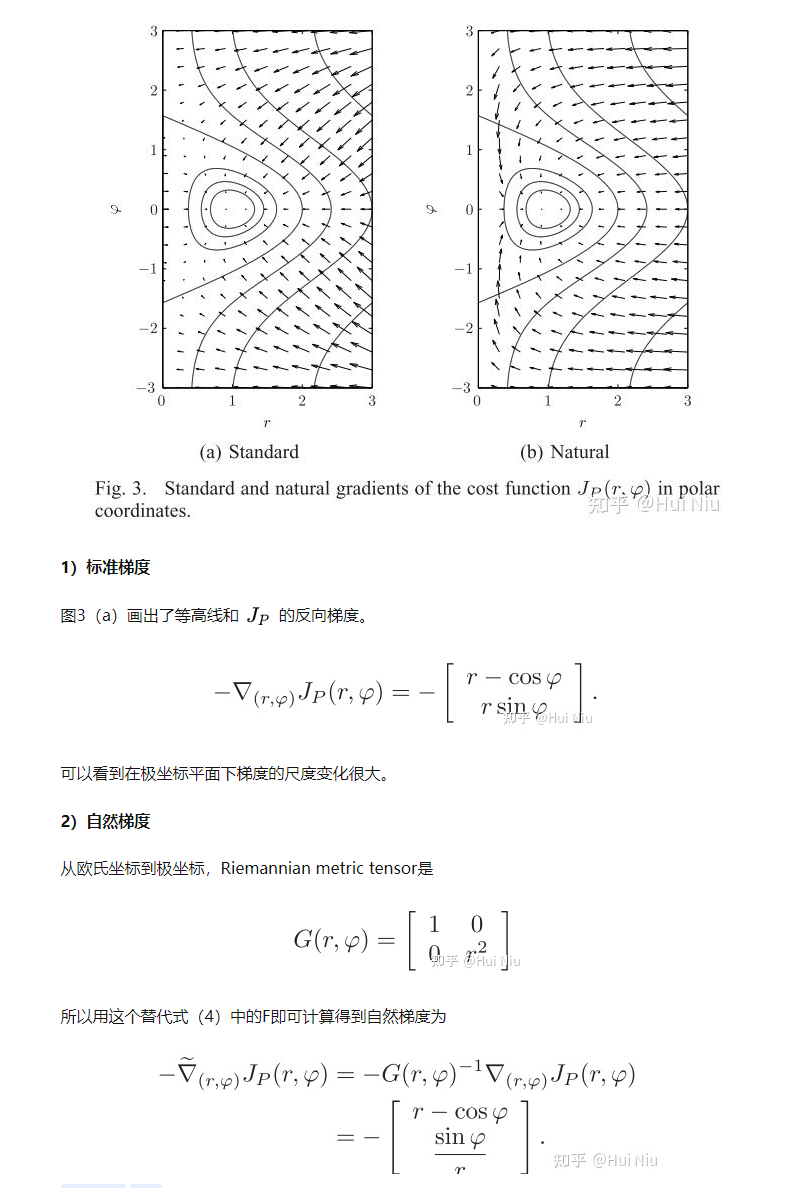
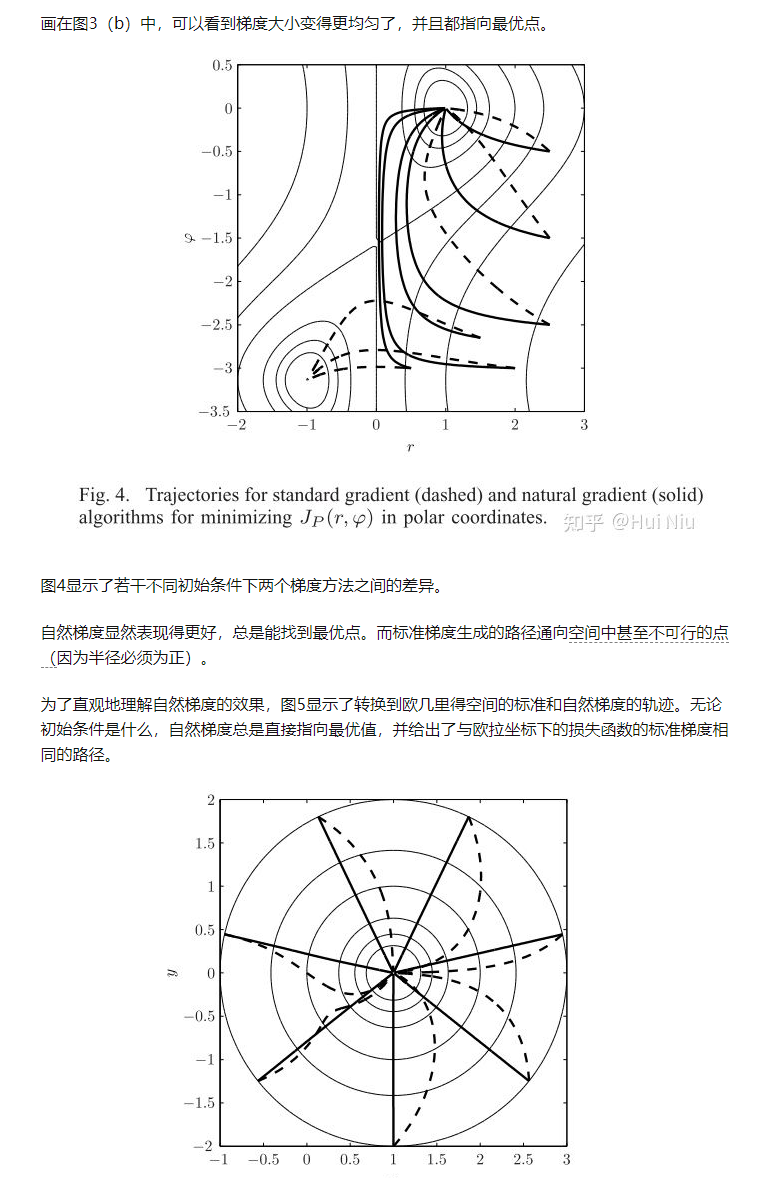
Similarity Measure

衡量两个概率分布的差异时，我们经常使用KL-divergence，而KL-divergence可以用Fisher Information matrix为tensor的metric来近似。

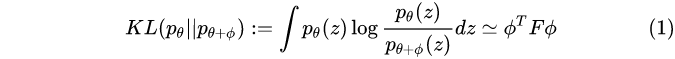
这里 F 是Fisher information matrix，

(1)式的推导过程如下

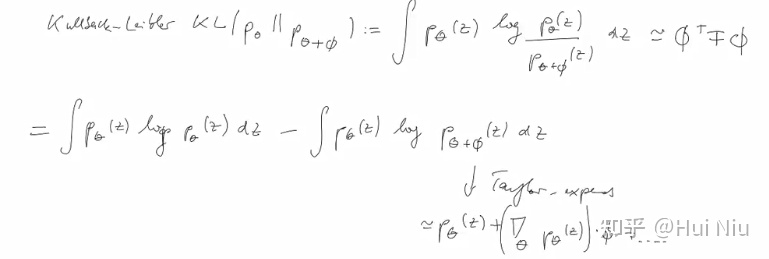
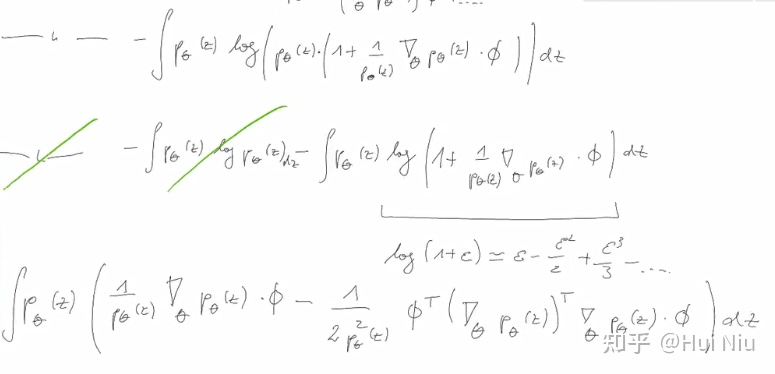
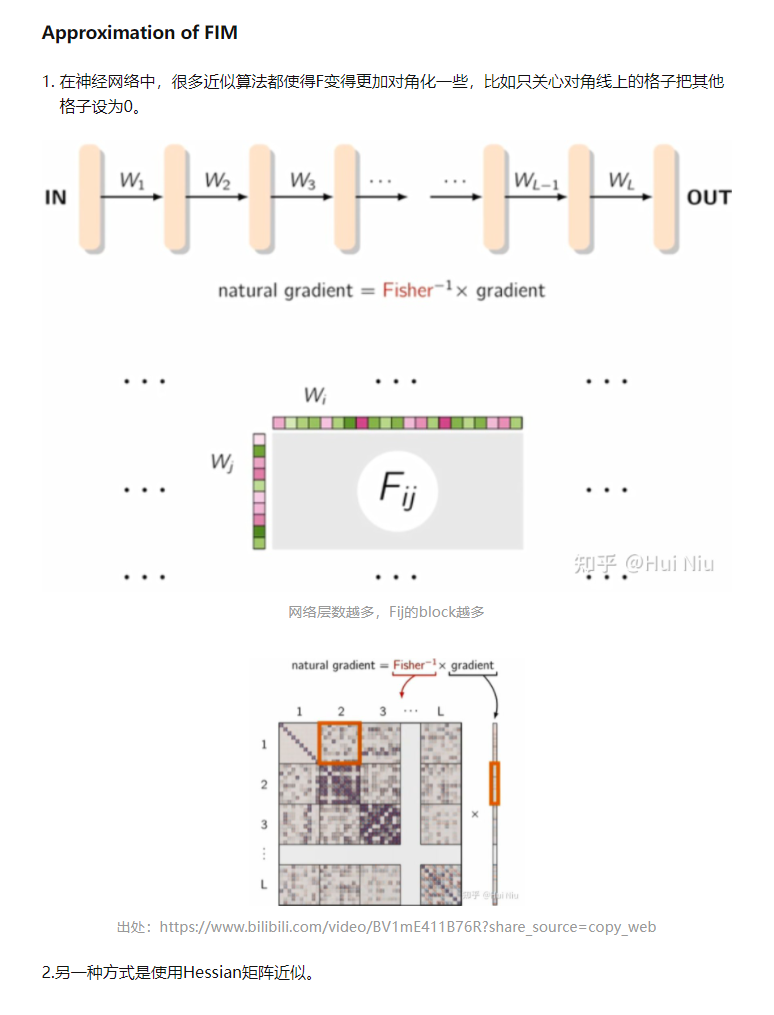
本文同步发表在我个人知乎： https://zhuanlan.zhihu.com/p/378642844