作者:张楚珩
链接:https://www.zhihu.com/question/45116323/answer/2276075256
来源:知乎
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
原文传送门
Hambly B, Xu R, Yang H. Recent Advances in Reinforcement Learning in Finance[J]. arXiv preprint arXiv:2112.04553, 2021.
特色
牛津大学发表的一个强化学习最新进展报告,推荐大家都去读一读:不仅很新(一周前),而且写的不错。特别是前面强化学习理论部分的总结是很全面的,即使只是关心强化学习理论的同学,也可以去那边看看(这部分我们这里不讲)。这篇综述里面讲了好几个应用,除了常见的交易执行、做市、资产组合之外,还讲了金融里面一些比较少见的应用,这里先只讲交易执行。
内容
一、强化学习 + 最优交易执行
任务描述和经典做法,本专栏前面有介绍过:张楚珩:【交易执行】Almgren-Chriss Model。
衡量指标:
- Profit and Loss (PnL) :交易过程中获取的整体收益;
- Implementation Shortfall:交易算法的总收益和全部在第一时间交易出去的总收益之差;
- Sharp ratio:平均收益除以收益标准差。
基准策略:
Time-Weighted Average Price(TWAP):在时间上均匀执行;
Volume-Weighted Average Price(VWAP):在交易量上均匀执行,准确得到相应的执行方案也是一个值得研究的问题;
Submit and Leave(SnL):挂一个固定的卖单,然后等它成交,如果最后成交不完,就全部市价卖出;
Almgren-Chriss:按照在一定价格运动假设下的最优解析策略执行。
注:我们这里着重讲交易执行,还有些文章研究如何从交易中盈利,这些文章我们不详细讲:
Jeong G, Kim H Y. Improving financial trading decisions using deep Q-learning: Predicting the number of shares, action strategies, and transfer learning[J]. Expert Systems with Applications, 2019, 117: 125-138.
Deng Y, Bao F, Kong Y, et al. Deep direct reinforcement learning for financial signal representation and trading[J]. IEEE transactions on neural networks and learning systems, 2016, 28(3): 653-664.
Zhang Z, Zohren S, Roberts S. Deep reinforcement learning for trading[J]. The Journal of Financial Data Science, 2020, 2(2): 25-40.
Wei H, Wang Y, Mangu L, et al. Model-based reinforcement learning for predictions and control for limit order books[J]. arXiv preprint arXiv:1910.03743, 2019. 张楚珩:【强化学习 187】Model-based RL for LOB
Shen Y, Huang R, Yan C, et al. Risk-averse reinforcement learning for algorithmic trading[C]//2014 IEEE Conference on Computational Intelligence for Financial Engineering & Economics (CIFEr). IEEE, 2014: 391-398. 额外会控制风险,讨论带风险控制的 DQN 方法。
下面列举一些经典的文章:
- Nevmyvaka Y, Feng Y, Kearns M. Reinforcement learning for optimized trade execution[C]//Proceedings of the 23rd international conference on Machine learning. 2006: 673-680.
比较经典的一篇文章,发表在 ICML-06,基本上基于 DQN 算法,不过对于时间点和剩余仓位等做了离散化,然后采取了提高学习效率的一些技巧(对于每个市场状态,都假设自己处于不同的私有状态下,进行相应 Q 值更新)。
- Hendricks D, Wilcox D. A reinforcement learning extension to the Almgren-Chriss framework for optimal trade execution[C]//2014 IEEE Conference on Computational Intelligence for Financial Engineering & Economics (CIFEr). IEEE, 2014: 457-464.
张楚珩:【强化学习 186】Almgren-Chriss + RL
- Ning B, Lin F H T, Jaimungal S. Double deep q-learning for optimal execution[J]. arXiv preprint arXiv:1812.06600, 2018.
张楚珩:【强化学习 158】RL Finance Application 里面有讲到。
- Ye Z, Deng W, Zhou S, et al. Optimal Trade Execution Based on Deep Deterministic Policy Gradient[C]//International Conference on Database Systems for Advanced Applications. Springer, Cham, 2020: 638-654.
主要使用了 DDPG 算法,唯一比较创新的地方是设计了 encoder 的特殊结构。
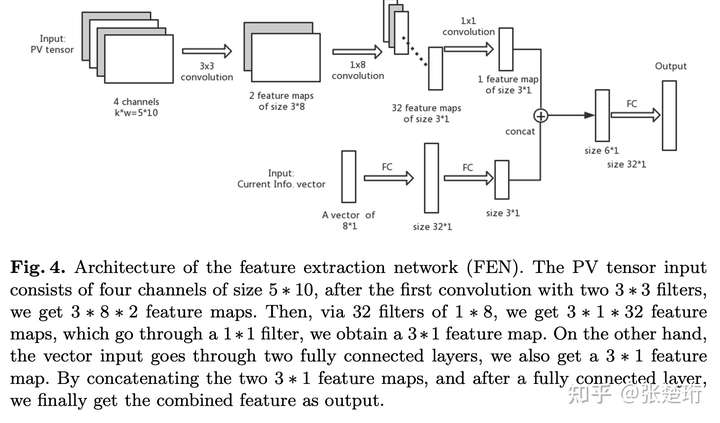
- Lin S, Beling P A. An End-to-End Optimal Trade Execution Framework based on Proximal Policy Optimization[C]//IJCAI. 2020: 4548-4554.
主要基于 PPO,在 encoder 上使用了 LSTM 和 Flatten+MLP 两种结构;不过实验效果上看起来两种差不多。奖励函数上使用了比较稀疏的奖励函数,即如果比基准 TWAP 算法好,就对于整个轨迹给正的奖励函数。即
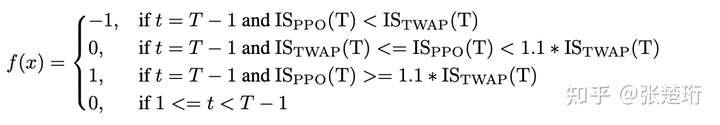
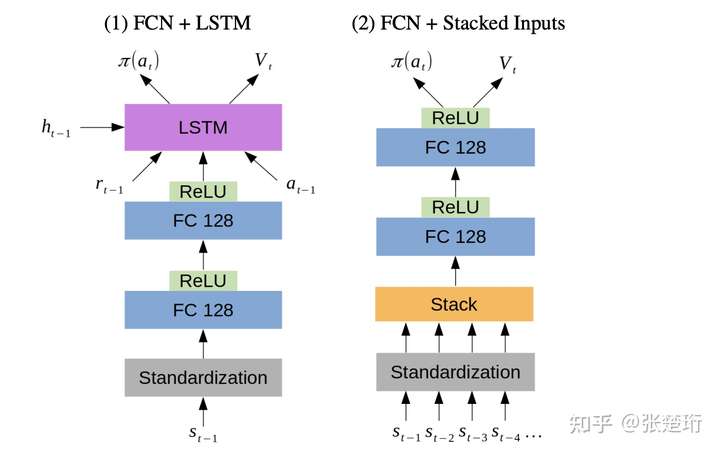
- Hambly B, Xu R, Yang H. Policy gradient methods for the noisy linear quadratic regulator over a finite horizon[J]. SIAM Journal on Control and Optimization, 2021, 59(5): 3359-3391.
虽然文章主要讲的是如何利用强化学习基于采样去求解 LQR 问题,不过里面一直用最有交易的例子在说明。首先最优交易执行能够被写成 LQR 问题的形式。
S 为价格,u 为交易量,q 为剩余交易量,Z 为随机变量,gamma 为价格冲击,sigma 为波动率。下面式子是价格和剩余交易量的运动规律
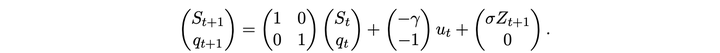
优化目标为 implementation shortfall
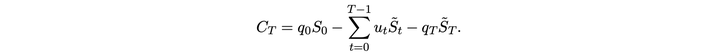
最终的优化目标如下:phi 是平衡收益和风险的变量,epsilon 是为了 LQR 问题有解(需要假设某矩阵的正定性)加上的一个小量。
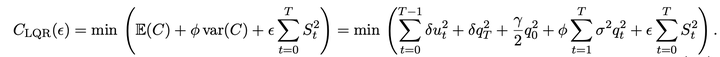
算法类似强化学习里面的 PG,每次把控制序列中的第 t 步换成一个新的数值,然后测量整个轨迹的好坏,最后根据此来计算梯度。其中 K 是被学习的控制策略,每次都从 K 附近做一个扰动 U 来形成一个新的控制轨迹 Khat。该算法那有 sample complexity 的理论保证。注意到该算法中是不需要定好相应参数(比如 sigma)的。

实验结果,使用的相对 implementation shortfall 来衡量的。
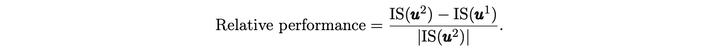
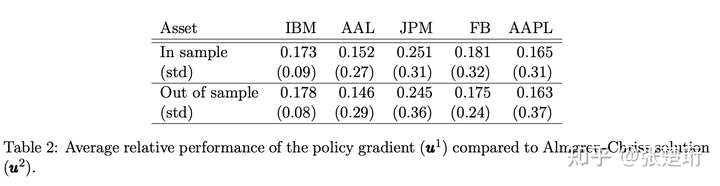
- Leal L, Laurière M, Lehalle C A. Learning a functional control for high-frequency finance[J]. arXiv preprint arXiv:2006.09611, 2020.
根据 [Cartea and Jaimungal 2016],可以在特定假设下结束最优执行问题的最优解。其中 S 为价格,alpha 和 sigma 为随机过程参数,nu 为交易速率,Delta t 为时间间隔,Q 为所剩仓位,kappa 为短期价格冲击参数,A 为末尾剩余未交易的惩罚系数,phi 为风险偏好系数。最后一行为解的大致形式。
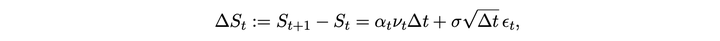
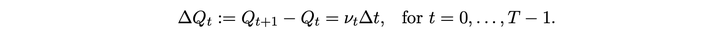
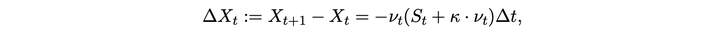

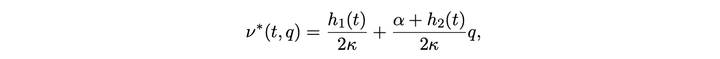
用神经网络 f 来产生相应的策略,则每一步状态转移如下
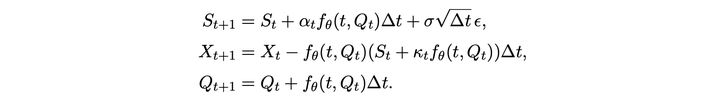
本文有以下几个重点:
希望学习到随着不同用户风险偏好而不同的相应策略,即这里的神经网络还将 A 和 phi 作为输入。
先在人造数据上学习,再迁移学习到真实历史数据上,从而提高样本使用效率。迁移的方式就是把训练好的神经网络来做初始化。
由于已知最优解形式,学习到神经网络后,可以把它投影到最优解的空间上,从而获取一定可解释性。
Dabérius K, Granat E, Karlsson P. Deep Execution-Value and Policy Based Reinforcement Learning for Trading and Beating Market Benchmarks[J]. Available at SSRN 3374766, 2019.
在模拟数据上跑的 DDQN 和 PPO。
- Bao W, Liu X. Multi-agent deep reinforcement learning for liquidation strategy analysis[J]. arXiv preprint arXiv:1906.11046, 2019. (ICML-19)
基于 Almgren-Chriss 模型构建了多智能体环境:
状态:包括过去若干天的价格,所剩的时间,以及每个智能体各自所剩仓位;不过对于每个智能体来讲,不能观察到其他智能体的仓位。
动作:每个智能体减仓的数量(所剩仓位乘以减仓比例);
奖励:从当前状态出发 Almgren-Chriss 最优策略下的效用函数(均值+λ标准差)的两步之间的差;通过基于后续最优策略下的效用函数值来计算,能减小奖励函数的 variance。
可观测状态:
算法使用多智能体的 DDPG,和普通 DDPG 的区别在于:1)对于每个只智能体维护 actor 和 critic 以及相应的 target network,其输入包括该智能体可观察到的状态;2)每个智能体使用单独的 replay buffer;3)不同智能体对应的 actor 和 critic 在每轮训练中得到更新。
文章说明了如下几件事情:
1)使用两个智能体一起执行得到的 implementation shortfall 比单独执行要更优,从而能够论证使用多智能体来建模解决最优执行问题的优势。

看了一下推导,个人感觉,两个智能体放到一起执行更优是来自于指标计算层面的,但是实际中并不会更优。这里假设两个智能体一起执行的时候,他们仍然面临着一样的、不受另一个智能体影响的价格序列,因为分散了仓位,因此计算出来的市场冲击更小,从而最优。但是实际情况并不是这样,假设在某个时间点智能体 1 交易了 n1,拿到了一个市场冲击 gamma × n1,那么智能体 2 再在此刻交易 n2 时,拿到的市场冲击肯定就不是 gamma × n2 了,因为智能体 1 已经把订单簿吃了一截了,智能体 2 拿到的价格只会更差。这跟把俩智能体放在一起交易是一样的。
这一块的实验结果如下,A 交易 1M 股,B1 和 B2 分别交易 0.3M 和 0.7M 股。
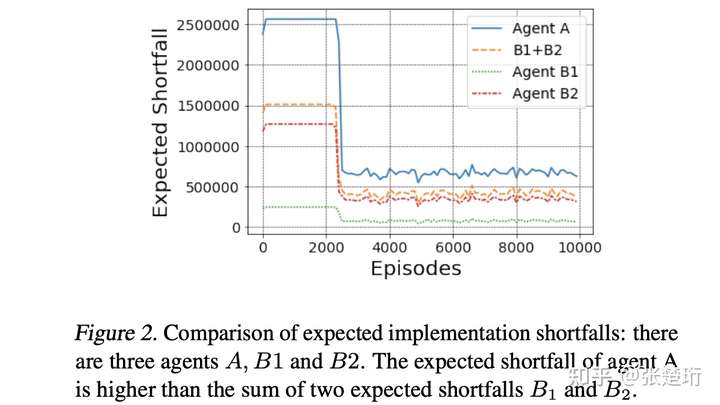
2)两个智能体在一起交易形成的最优轨迹和单独交易的最优轨迹不一样,从而说明搞多智能体的 non-trivialty。

文章没有写 x 是啥,我猜是如果把两个智能体放到一起交易时,最优的所剩仓位轨迹(两个智能体所剩仓位加起来)。关于这一点,个人感觉还是挺奇怪的:看一下推导可以发现,这里所形成轨迹不一样的原因是两个智能体放到一起交易的时候,他们优化的目标是下面这个综合的效用函数,即智能体 1 的策略选择,其实还要关注智能体 2 的目标(其中包括了智能体 2 的风险偏好)。
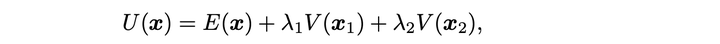
类似的真正有用的结论应该是说通过在市场环境中的相互作用,而导致不同风险偏好的智能体相互有影响,并且形成新的均衡。
实验结果如下,其中 A1、A2 是单独交易,B1、B2 是在一起交易,风险偏好分别是 1e-4 和 1e-9。这里的实验看起来和理论也不是太一致,理论是目标放到一起优化,而实验是单独设置的奖励函数,我没太想明白,单独设置奖励函数的话,如何能达到这样的效果。目前猜测是 permanent market impact 上两个智能体会相互影响。
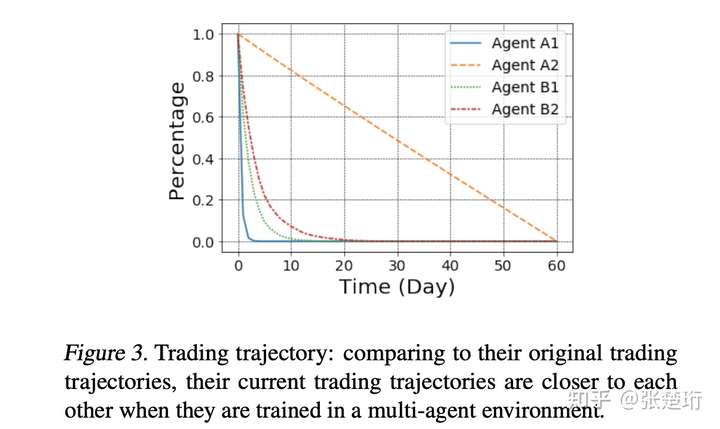
3)可以通过设置合作型或者竞争型的奖励函数,使得智能体之间能够竞争或者合作。
合作型奖励函数为
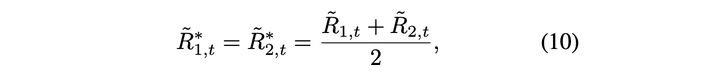
竞争型奖励函数为

实验上发现合作型的影响不太大,竞争型的会有区别。个人感觉可能是原来的环境就搞成合作型的了。
- Karpe M, Fang J, Ma Z, et al. Multi-agent reinforcement learning in a realistic limit order book market simulation[J]. arXiv preprint arXiv:2006.05574, 2020.
张楚珩:【强化学习 188】ABIDES
编辑于 2021-12-18 11:23
赞同 160添加评论分享收藏喜欢收起
更多回答

BigQuant
BigQuant.com 让每个投资者用上AI
50 人赞同了该回答
首先,强化学习和(无)监督学习并不是完全分开的概念,强化学习的很多方法中都用到了监督学习,比如DQN。
监督学习中要求数据集是独立同分布的,但由于金融数据集的特殊性,有时候并不能满足这一要求,这时候如果直接把监督学习应用到金融数据集上,就可能会导致很多问题。而强化学习并没有这样的要求假设。
监督学习模型相当于是输入输出之间的一个黑盒子,模型的可解释性较低,而强化学习在某一个状态下采取某种行为,获得某些奖励,根据奖励反馈来对行为进行比较选择的这种逻辑,与在金融市场上进行买卖操作的逻辑也是一致的。
以下是一些具体应用的方向,感兴趣的朋友可以在BigQuant AI平台上动手实践一下,并且很快可视化的强化学习模块也要在平台上线了,敬请期待。
1. 相比(无)监督学习,强化学习在量化领域应用时,首先需要建立一个环境,在环境中定义state,action,以及reward等。定义的方式有多种选择,比如:
state: 可以将n天的价格,交易量数据组合成某一天的state,也可以用收益率或是其他因子组合作为某一天的state,如果想要定义有限个的state,可以定义为appreciated/ hold_value/ depreciated这样3类。
action: 可以定义为buy/sell两种, 也可以定义为buy/sell/hold三种,或者定义为一个(-1,1)之间的一个连续的数,-1和1分别代表all out 和 holder两个极端。
reward: 可以定义为新旧总资产价值之间的差,或是变化率,也可以将buy时的reward定义为0,sell时的定义为买卖价差。
2. 需要选择一个具体的强化学习方法:
1) Q-table (具体可参考:Reinforcement Learning Stock Trader)
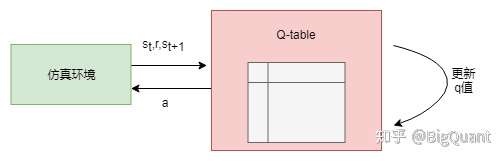
个人认为这不是一个很好的办法,因为Q-table里面的state是有限的,而我们定义的state里面的数据往往都是连续的,很难在有限个state里面去很好的表达。
2) Deep Q Network(参考:Reinforcement Learning for Stock Prediction )
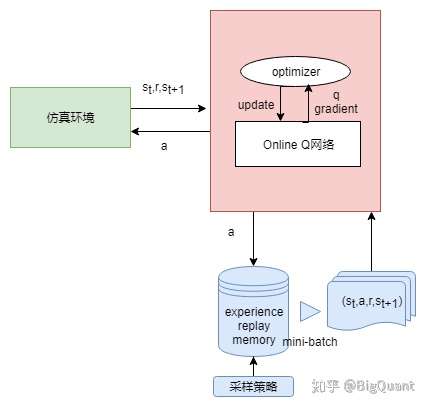
在1的基础上,将Q-table的功能用一个深度学习网络来实现,解决了有限个state的问题。
3) Actor Critic (参考:Deep-Reinforcement-Learning-in-Stock-Trading)
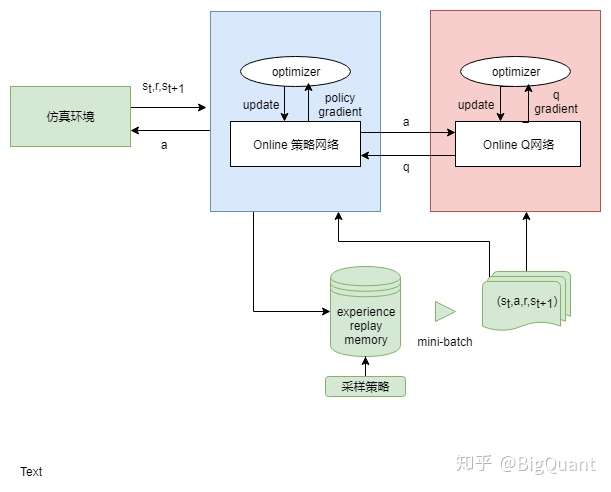
用两个模型,一个同DQN输出Q值,另一个直接输出行为。但由于两个模型参数更新相互影响,较难收敛。
4) DDPG(参考:ml-stock-prediction)
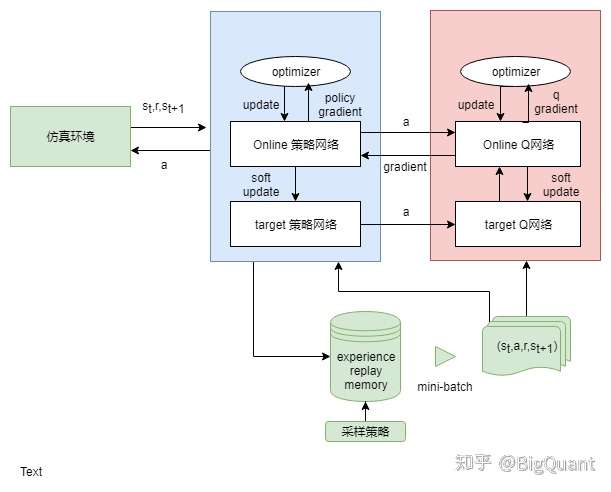
加入了不及时更新参数的模型,解决难收敛的问题
3. 由于多数方法中都用到了深度神经网络,我们还需要对神经网络的模型,深度,还有其他参数进行一个选择。
4. 比较简单的应用逻辑是对单个股票某一时间段进行择时,如果需要也可以在这个基础上进行一些调整,对某个股票池的股票进行分析,调整为一个选股策略。