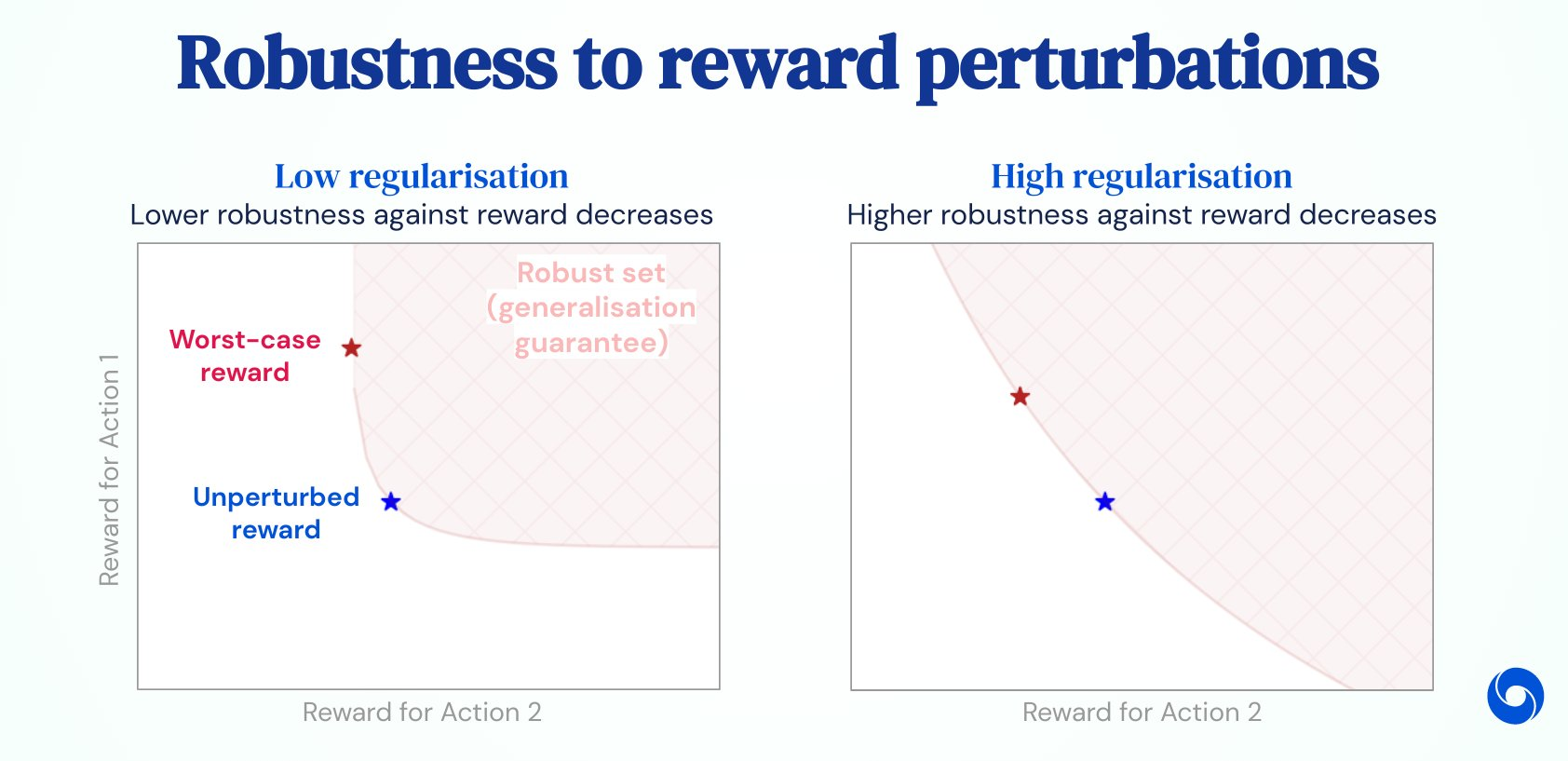
Policy regularization methods such as maximum entropy regularization are widely used in reinforcement learning to improve the robustness of a learned policy. In this paper, we show how this robustness arises from hedging against worst-case perturbations of the reward function, which are chosen from a limited set by an imagined adversary. Using convex duality, we characterize this robust set of adversarial reward perturbations under kl- and α-divergence regularization, which includes Shannon and Tsallis entropy regularization as special cases. Importantly, generalization guarantees can be given within this robust set. We provide detailed discussion of the worst-case reward perturbations, and present intuitive empirical examples to illustrate this robustness and its relationship with generalization. Finally, we discuss how our analysis complements and extends previous results on adversarial reward robustness and path consistency optimality conditions.
论文: https://arxiv.org/pdf/2203.12592.pdf
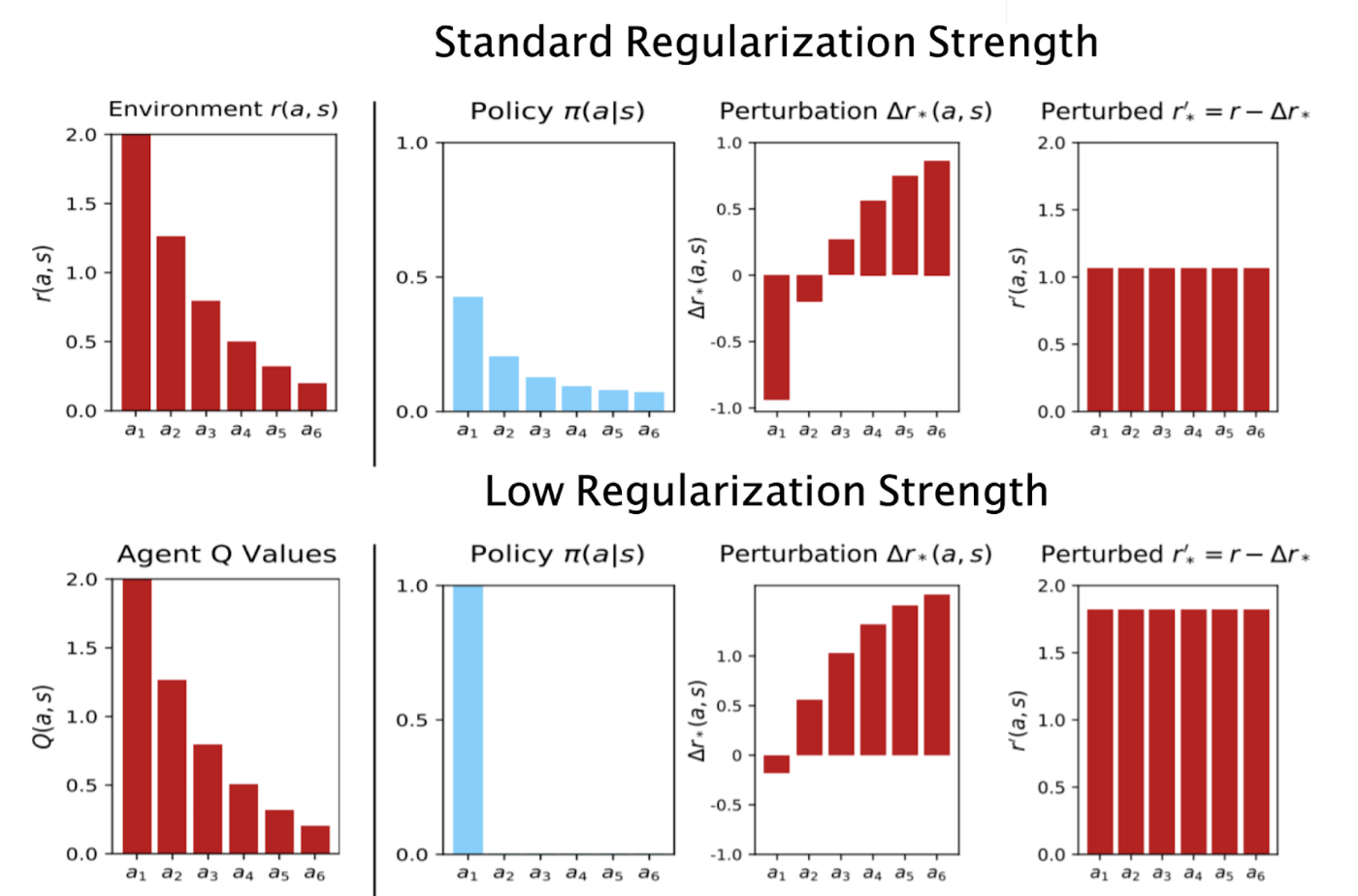
上面显示的几乎不规则的策略(第二列,底部)几乎确定性地选择了最高回报的行动;减少此动作的奖励对对手来说非常“昂贵”,但即使是很小的减少也会对预期奖励产生影响。相反,低概率行为的奖励扰动需要更大才能产生影响(并且可以解释为对对手来说“更便宜”)。代理和对手之间的 mini-max 博弈的解决方案以无差异为特征,如第四列所示。在(最优)扰动奖励函数下,代理没有动力改变其策略以增加或减少任何行动的可能性,因为它们都会产生相同的扰动奖励——在考虑了对手的最佳策略后,最佳代理会为其每个行动获得相同的价值。(请注意,这种无差异并不意味着代理选择具有统一概率的动作。)
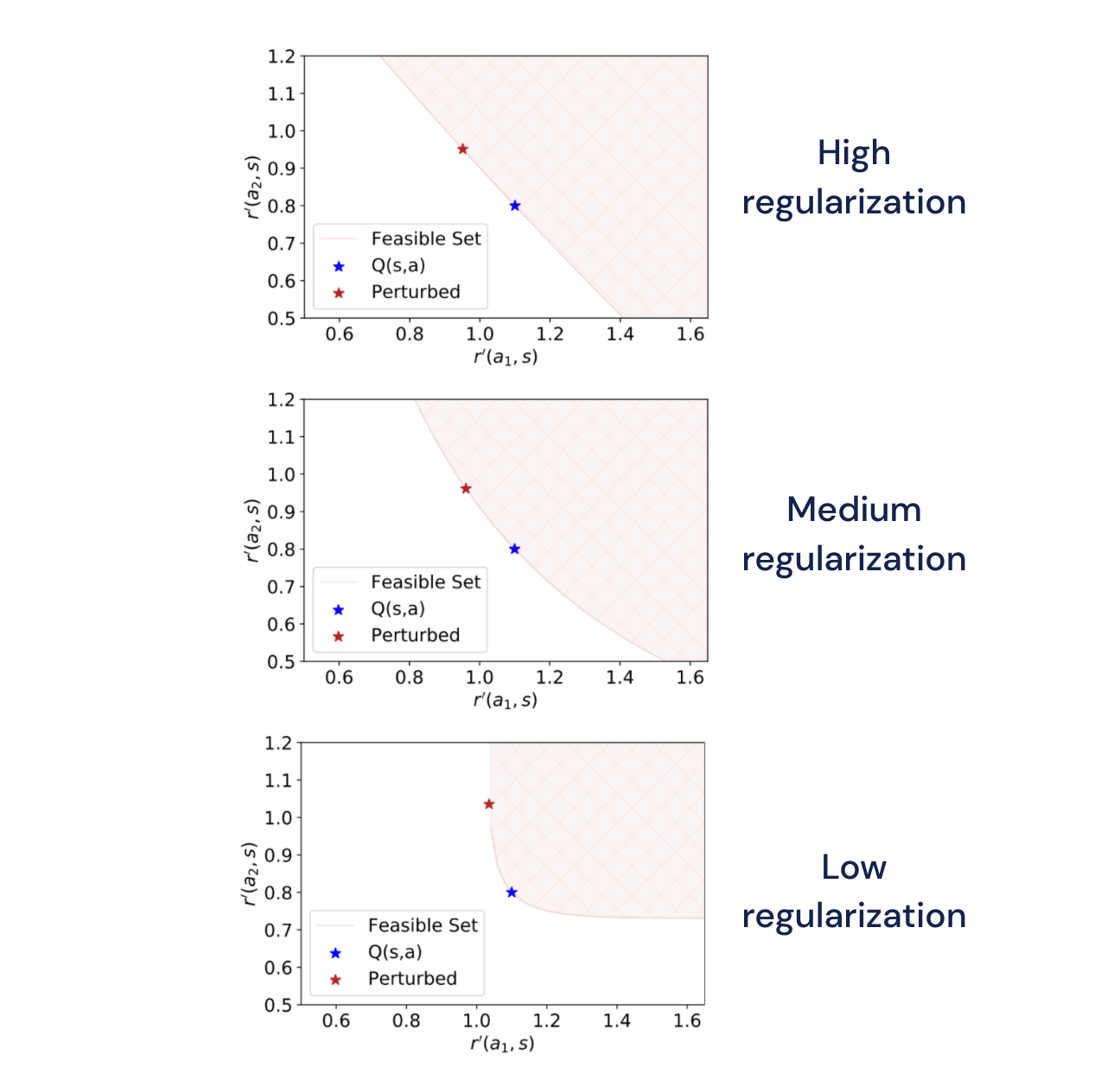
可行集(红色区域)**:**对于单个状态和两个动作的各种正则化器强度,对手可用的一组扰动。X 轴和 Y 轴分别显示每个动作的扰动奖励。蓝色星表示未受扰动的奖励(所有图中的值相同),红色星表示在最坏情况下奖励扰动下的奖励(更多详细信息请参阅论文)。对于可行集中的每个扰动,正则化策略保证获得大于或等于正则化目标值的预期扰动奖励。正如直观预期的那样,随着正则化强度的降低,可行集变得更加受限,这意味着生成的策略变得不那么健壮(尤其是在奖励减少的情况下)