TRPO文章中描述先前的工作通过使用旧策略的状态访问频率 代替 新策略的状态访问频率,其本质是一阶近似。也就是说通过一阶展开找到原目标函数的上限。为了使得策略相差不大,使用mixture策略进行策略更新,
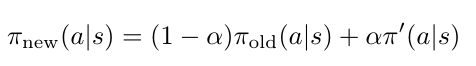
该mixture策略提升的下限为,
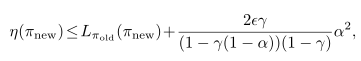
不等式最右边部分指的是基于原策略采样,应用mixture策略的回报上限吗?
然后,作者使用TV散度,TV散度和KL散度的关系进行推导得到如下公式
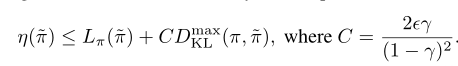
在算法迭代过程中,如下所示

策略 $\pi_{i}$ 的回报是递减的,如上公式所示。这里我很不明白为什么递减。按照我的理解,进行策略迭代是找到策略 $\pi$ 能够提高原目标函数值。不应该是递增的吗。